如图，一次函数 $y=mx+4$ 的图象与二次函数 $y=\dfrac 14x^2$ 的图象交于 $A\left({x_1},{y_1}\right)$，$B\left({x_2},{y_2}\right)$ 两点．试判断 $\triangle AOB$ 的形状，并证明．
【难度】
【出处】
无
【标注】
【答案】
$\triangle AOB$ 为直角三角形
【解析】
联立方程组 $\begin{cases} y=mx+4, \\ y=\dfrac 14x^2,\end{cases}$
解得 $\begin{cases}x_1=2m-2\sqrt {m^2+4}, \\ y_1=\left(m-\sqrt {m^2+4}\right)^2,\end{cases}\begin{cases} x_2=2m+2\sqrt {m^2+4}, \\ y_2=\left(m+\sqrt {m^2+4}\right)^2. \end{cases}$
所以点 $A\left(2m-2\sqrt {m^2+4},\left(m-\sqrt {m^2+4}\right)^2\right)$，点 $B\left(2m+2\sqrt {m^2+4},\left(m+\sqrt {m^2+4}\right)^2\right)$．
如图，过 $A,B$ 两点作 $x$ 轴的垂线，垂足分别为 $C,D$．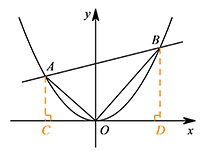
则 $AC=\left(m-\sqrt {m^2+4}\right)^2$，$OC=-\left(2m-2\sqrt {m^2+4}\right)$，
$BD=\left(m+\sqrt {m^2+4}\right)^2$，$OD=2m+2\sqrt {m^2+4}$．
所以 $\dfrac {AC}{OC}=\dfrac {OD}{BD}=-\dfrac {m-\sqrt {m^2+4}}{2}$．
而 $\angle ACO=\angle ODB=90^\circ$，
所以 $\triangle ACO\backsim \triangle ODB$．
所以 $\angle AOC=\angle OBD$．
又 $\angle OBD+\angle BOD=90^\circ$，
所以 $\angle AOC+\angle BOD=90^\circ$，
即 $\angle AOB=90^\circ$，$\triangle AOB$ 为直角三角形．
解得 $\begin{cases}x_1=2m-2\sqrt {m^2+4}, \\ y_1=\left(m-\sqrt {m^2+4}\right)^2,\end{cases}\begin{cases} x_2=2m+2\sqrt {m^2+4}, \\ y_2=\left(m+\sqrt {m^2+4}\right)^2. \end{cases}$
所以点 $A\left(2m-2\sqrt {m^2+4},\left(m-\sqrt {m^2+4}\right)^2\right)$，点 $B\left(2m+2\sqrt {m^2+4},\left(m+\sqrt {m^2+4}\right)^2\right)$．
如图，过 $A,B$ 两点作 $x$ 轴的垂线，垂足分别为 $C,D$．
则 $AC=\left(m-\sqrt {m^2+4}\right)^2$，$OC=-\left(2m-2\sqrt {m^2+4}\right)$，$BD=\left(m+\sqrt {m^2+4}\right)^2$，$OD=2m+2\sqrt {m^2+4}$．
所以 $\dfrac {AC}{OC}=\dfrac {OD}{BD}=-\dfrac {m-\sqrt {m^2+4}}{2}$．
而 $\angle ACO=\angle ODB=90^\circ$，
所以 $\triangle ACO\backsim \triangle ODB$．
所以 $\angle AOC=\angle OBD$．
又 $\angle OBD+\angle BOD=90^\circ$，
所以 $\angle AOC+\angle BOD=90^\circ$，
即 $\angle AOB=90^\circ$，$\triangle AOB$ 为直角三角形．
答案
解析
备注
