如图，在平面直角坐标系中，点 $O$ 为坐标原点，直线 $l$ 与抛物线 $y=-\sqrt 3x^2+4\sqrt 3x$ 相交于 $A\left(1,3\sqrt 3\right)$，$B\left(4,0\right)$ 两点．在坐标轴上是否存在点 $D$，使得 $\triangle ABD$ 是以线段 $AB$ 为斜边的直角三角形．若存在，求出点 $D$ 的坐标；若不存在，说明理由．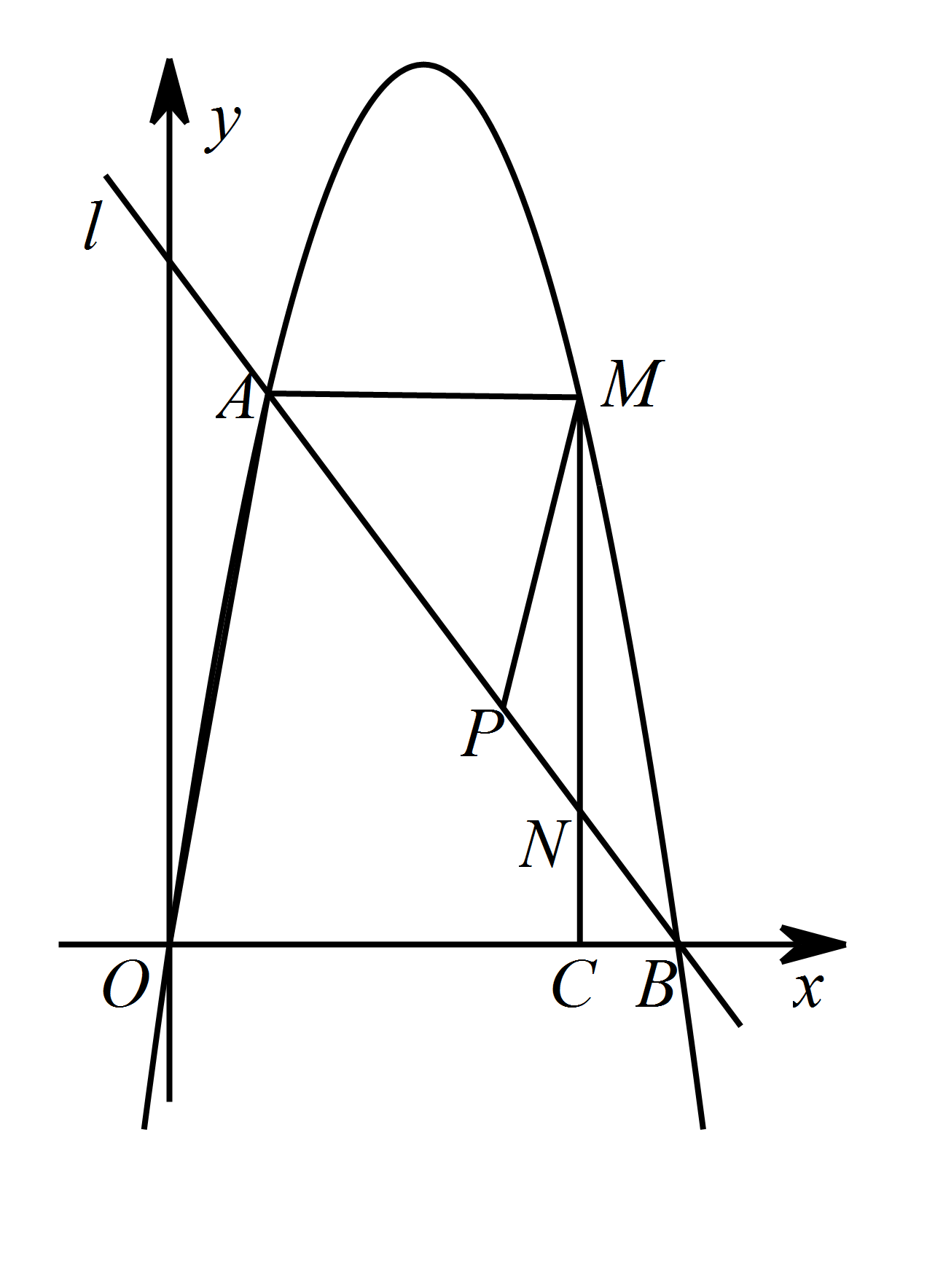
【难度】
【出处】
无
【标注】
【答案】
存在，点 $D$ 的坐标为 $\left(1,0\right)$，$\left(0,\dfrac {3\sqrt 3+\sqrt {11}} 2 \right)$ 或 $\left(0,\dfrac {3\sqrt 3-\sqrt {11}} 2 \right)$
【解析】
① 当点 $D$ 在 $x$ 轴上时，过点 $A$ 作 $AD\perp x$ 轴于点 $D$，
因为点 $A\left(1,3\sqrt 3\right)$，
所以点 $D$ 坐标为 $\left(1,0\right)$；
② 当点 $D$ 在 $y$ 轴上时，设点 $D\left(0,d\right)$，则：
$AD^2=1+\left(3\sqrt 3-d\right)^2$，$BD^2=4^2+d^2$，
$AB^2=\left(4-1\right)^2+\left(3\sqrt 3\right)^2=36$，
因为 $\triangle ABD$ 是以 $AB$ 为斜边的直角三角形，
所以 $AD^2+BD^2=AB^2$，
即 $1+\left(3\sqrt 3-d\right)^2+4^2+d^2=36$，
解得 $d=\dfrac {3\sqrt 3\pm \sqrt {11}}2$．
所以点 $D$ 的坐标为 $\left(1,0\right)$，$\left(0,\dfrac {3\sqrt 3+\sqrt {11}} 2 \right)$ 或 $\left(0,\dfrac {3\sqrt 3-\sqrt {11}} 2 \right)$．
因为点 $A\left(1,3\sqrt 3\right)$，所以点 $D$ 坐标为 $\left(1,0\right)$；
② 当点 $D$ 在 $y$ 轴上时，设点 $D\left(0,d\right)$，则：
$AD^2=1+\left(3\sqrt 3-d\right)^2$，$BD^2=4^2+d^2$，
$AB^2=\left(4-1\right)^2+\left(3\sqrt 3\right)^2=36$，
因为 $\triangle ABD$ 是以 $AB$ 为斜边的直角三角形，
所以 $AD^2+BD^2=AB^2$，
即 $1+\left(3\sqrt 3-d\right)^2+4^2+d^2=36$，
解得 $d=\dfrac {3\sqrt 3\pm \sqrt {11}}2$．
所以点 $D$ 的坐标为 $\left(1,0\right)$，$\left(0,\dfrac {3\sqrt 3+\sqrt {11}} 2 \right)$ 或 $\left(0,\dfrac {3\sqrt 3-\sqrt {11}} 2 \right)$．
答案
解析
备注
