如图，正比例函数 $y=2x$ 的图象与反比例函数 $y=\dfrac{k}{x}$ 的图象交于 $A,B$ 两点，过点 $A$ 作 $AC$ 垂直 $x$ 轴于点 $C$，连接 $BC$．若 $\triangle ABC$ 的面积为 $2$．$x$ 轴上是否存在一点 $D$，使 $\triangle ABD$ 为直角三角形？若存在，求出点 $D$ 的坐标，若不存在，请说明理由．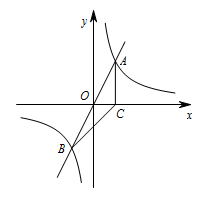
【难度】
【出处】
无
【标注】
【答案】
存在，点 $D$ 的坐标为 $\left(\sqrt 5,0\right)$，$\left(-\sqrt 5,0\right)$，$\left(-5,0\right)$ 或 $\left(5,0\right)$
【解析】
因为正比例函数与反比例函数的两个交点关于原点对称，
所以 $S_{\triangle AOC}=S_{\triangle BOC}=\dfrac 12S_{\triangle ABC}=1$．
而 $AC$ 垂直 $x$ 轴，所以 $k=2$，
即反比例函数为 $y=\dfrac 2x$．
所以点 $A\left(1,2\right)$，点 $B\left(-1,-2\right)$，
所以 $AB=\sqrt {\left(1+1\right)^2+\left(2+2\right)^2}=2\sqrt 5$．
假设存在这样的 $D$ 点，设 $D$ 的坐标为 $\left(m,0\right)$，
则 $AD=\sqrt {\left(1-m\right)^2+2^2}$，$BD=\sqrt {\left(m+1\right)^2+2^2}$．
① 如图，当点 $D$ 为直角顶点，且 $D$ 在 $x$ 轴正半轴时，
由 $AB=2\sqrt 5$，所以 $OD=\dfrac 12AB=\sqrt 5$，
所以此时点 $D$ 的坐标为 $\left(\sqrt 5,0\right)$ 或 $\left(-\sqrt 5,0\right)$；
② 当 $A$ 为直角顶点时，则点 $D$ 在 $x$ 轴正半轴．
由 $AB^2+AD^2=BD^2$，得 $\left(2\sqrt 5\right)^2+\left(1-m\right)^2+2^2=\left(1+m\right)^2+2^2$，
解得 $m=5$，所以此时点 $D$ 的坐标为 $\left(5,0\right)$；
③ 当 $B$ 为直角顶点时，则点 $D$ 在 $x$ 轴负半轴．
由 $BD^2+AB^2=AD^2$，得 $\left(2\sqrt 5\right)^2+\left(1+m\right)^2+2^2=\left(1-m\right)^2+2^2$，
解得 $m=-5$，所以此时点 $D$ 的坐标为 $\left(-5,0\right)$．
所以存在这样的点 $D$，使 $\triangle ABD$ 为直角三角形，点 $D$ 的坐标为 $\left(\sqrt 5,0\right)$，$\left(-\sqrt 5,0\right)$，$\left(-5,0\right)$ 或 $\left(5,0\right)$．
所以 $S_{\triangle AOC}=S_{\triangle BOC}=\dfrac 12S_{\triangle ABC}=1$．
而 $AC$ 垂直 $x$ 轴，所以 $k=2$，
即反比例函数为 $y=\dfrac 2x$．
所以点 $A\left(1,2\right)$，点 $B\left(-1,-2\right)$，
所以 $AB=\sqrt {\left(1+1\right)^2+\left(2+2\right)^2}=2\sqrt 5$．
假设存在这样的 $D$ 点，设 $D$ 的坐标为 $\left(m,0\right)$，
则 $AD=\sqrt {\left(1-m\right)^2+2^2}$，$BD=\sqrt {\left(m+1\right)^2+2^2}$．
① 如图，当点 $D$ 为直角顶点，且 $D$ 在 $x$ 轴正半轴时，
由 $AB=2\sqrt 5$，所以 $OD=\dfrac 12AB=\sqrt 5$，所以此时点 $D$ 的坐标为 $\left(\sqrt 5,0\right)$ 或 $\left(-\sqrt 5,0\right)$；
② 当 $A$ 为直角顶点时，则点 $D$ 在 $x$ 轴正半轴．
由 $AB^2+AD^2=BD^2$，得 $\left(2\sqrt 5\right)^2+\left(1-m\right)^2+2^2=\left(1+m\right)^2+2^2$，解得 $m=5$，所以此时点 $D$ 的坐标为 $\left(5,0\right)$；
③ 当 $B$ 为直角顶点时，则点 $D$ 在 $x$ 轴负半轴．
由 $BD^2+AB^2=AD^2$，得 $\left(2\sqrt 5\right)^2+\left(1+m\right)^2+2^2=\left(1-m\right)^2+2^2$，解得 $m=-5$，所以此时点 $D$ 的坐标为 $\left(-5,0\right)$．
所以存在这样的点 $D$，使 $\triangle ABD$ 为直角三角形，点 $D$ 的坐标为 $\left(\sqrt 5,0\right)$，$\left(-\sqrt 5,0\right)$，$\left(-5,0\right)$ 或 $\left(5,0\right)$．
答案
解析
备注
