如图，抛物线 $L:y=ax^2+bx+c$ 与 $x$ 轴交于 $A,B(3,0) $ 两点（$A$ 在 $B$ 的左侧），与 $y$ 轴交于点 $C(0,3) $，已知对称轴 $x=1$．设点 $P$ 是抛物线 $L$ 上任一点，点 $Q$ 在直线 $l:x=-3$ 上，$\triangle PBQ$ 能否成为以点 $P$ 为直角顶点的等腰直角三角形？若能，求出符合条件的点 $P$ 的坐标；若不能，请说明理由．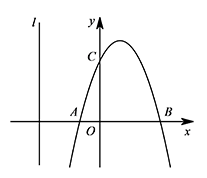
【难度】
【出处】
无
【标注】
【答案】
能，点 $P$ 的坐标为 $(0,3)$，$(1,4)$，$\left(\dfrac{3+\sqrt{33}}{2},\dfrac{-9-\sqrt{33}}{2}\right)$ 或 $\left(\dfrac{3-\sqrt{33}}{2},\dfrac{-9+\sqrt{33}}{2}\right)$
【解析】
由题意可得点 $A$ 的坐标为 $(-1,0)$．
所以抛物线解析式可变为 $y=a(x+1)(x-3)=ax^2-2ax-3a$，
由点 $C$ 的坐标可得 $-3a=3$，即 $a=-1$．
所以抛物线的解析式为 $y=-x^2+2x+3$．
如图，过 $P$ 点作 $PM$ 垂直于 $y$ 轴，垂足为点 $M$，过 $B$ 点作 $BN$ 垂直于直线 $PM$，垂足为点 $N$．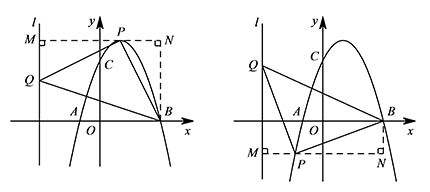
若 $\triangle PBQ$ 是以点 $P$ 为直角顶点的等腰直角三角形，
无论点 $P$ 在 $BQ$ 的上方或下方，由“弦图模型”均可得 $\triangle PQM\cong \triangle BPN$，
所以 $PM=BN$．
设点 $P$ 的坐标为 $(m,-m^2+2m+3)$，则 $PM=|m+3|$，$BN=|-m^2+2m+3|$．
所以 $|m+3|=|-m^2+2m+3|$，
解得 $m_1=0$，$m_2=1$，$m_3=\dfrac{3+\sqrt{33}}{2}$，$m_4=\dfrac{3-\sqrt{33}}{2}$．
所以点 $P$ 的坐标为 $(0,3)$，$(1,4)$，$\left(\dfrac{3+\sqrt{33}}{2},\dfrac{-9-\sqrt{33}}{2}\right)$ 或 $\left(\dfrac{3-\sqrt{33}}{2},\dfrac{-9+\sqrt{33}}{2}\right)$．
所以抛物线解析式可变为 $y=a(x+1)(x-3)=ax^2-2ax-3a$，
由点 $C$ 的坐标可得 $-3a=3$，即 $a=-1$．
所以抛物线的解析式为 $y=-x^2+2x+3$．
如图，过 $P$ 点作 $PM$ 垂直于 $y$ 轴，垂足为点 $M$，过 $B$ 点作 $BN$ 垂直于直线 $PM$，垂足为点 $N$．
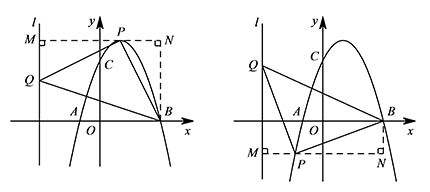若 $\triangle PBQ$ 是以点 $P$ 为直角顶点的等腰直角三角形，无论点 $P$ 在 $BQ$ 的上方或下方，由“弦图模型”均可得 $\triangle PQM\cong \triangle BPN$，
所以 $PM=BN$．
设点 $P$ 的坐标为 $(m,-m^2+2m+3)$，则 $PM=|m+3|$，$BN=|-m^2+2m+3|$．
所以 $|m+3|=|-m^2+2m+3|$，
解得 $m_1=0$，$m_2=1$，$m_3=\dfrac{3+\sqrt{33}}{2}$，$m_4=\dfrac{3-\sqrt{33}}{2}$．
所以点 $P$ 的坐标为 $(0,3)$，$(1,4)$，$\left(\dfrac{3+\sqrt{33}}{2},\dfrac{-9-\sqrt{33}}{2}\right)$ 或 $\left(\dfrac{3-\sqrt{33}}{2},\dfrac{-9+\sqrt{33}}{2}\right)$．
答案
解析
备注
