如图,$\triangle ABC$ 为直角三角形,$\angle ACB=90^\circ$,$AC=BC$,点 $A$、$C$ 在 $x$ 轴上,点 $B$ 坐标 $\left(3,m\right)$($m>0$),线段 $AB$ 与 $y$ 轴相交于点 $D$,以 $P\left(1,0\right)$ 为顶点的抛物线过点 $B$,$D$.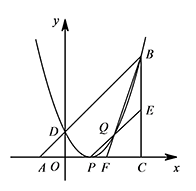
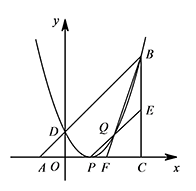
【难度】
【出处】
无
【标注】
-
求点 $A$ 的坐标(用 $m$ 表示);标注答案点 $A$ 的坐标为 $\left(3-m,0\right)$解析由 $B\left(3,m\right)$ 可知 $OC=3$,$BC=m$,
因为 $\triangle ABC$ 为等腰直角三角形.
所以 $AC=BC=m,OA=m-3$,
所以点 $A$ 的坐标为 $\left(3-m,0\right)$. -
求出抛物线的解析式;标注答案抛物线的解析式为 $y=x^2-2x+1$解析因为 $\angle ODA=\angle OAD=45^\circ$,
所以 $OD=OA=m-3$.
则点 $D$ 的坐标是 $\left(0,m-3\right)$.
因为抛物线顶点为 $P\left(1,0\right)$,且过点 $B$、$D$,
所以设抛物线的解析式为 $y=a\left(x-1\right)^2$.
依题意得 $\begin{cases}a\left(3-1\right)^2=m,\\a\left(0-1\right)^2=m-3.\end{cases}$
解得 $\begin{cases}a=1,\\m=4.\end{cases}$
所以 抛物线的解析式为 $y=x^2-2x+1$. -
设点 $Q$ 为抛物线上点 $P$ 至点 $B$ 之间的一动点,连接 $PQ$ 并延长,交 $BC$ 于点 $E$,连接 $BQ$ 并延长交 $AC$ 于点 $F$,证明 $FC\left(AC+EC\right)$ 的值为定值.标注答案为定值解析过点 $Q$ 作 $QM\perp AC$ 于点 $M$,过点 $Q$ 作 $QN\perp BC$ 于点 $N$,
设点 $Q$ 的坐标为 $\left(x,x^2-2x+1\right)$,
则 $QM=CN=\left(x-1\right)^2,MC=QN=3-x$.
因为 $m=4$,所以 $BC=AC=4$.
因为 $QM\parallel CE$,所以 $\triangle PQM\backsim \triangle PEC$.
所以 $\dfrac{QM}{EC}=\dfrac{PM}{PC}$,
即 $\dfrac{\left(x-1\right)^2}{EC}=\dfrac{x-1}{2}$,
得 $EC=2\left(x-1\right)$.
因为 $QN\parallel FC$,所以 $\triangle BQN\backsim \triangle BFC$.
所以 $\dfrac{QN}{FC}=\dfrac{BN}{BC}$,
即 $\dfrac{3-x}{FC}=\dfrac{4-\left(x-1\right)^2}{4}$,
得 $FC=\dfrac{4}{x+1}$.
因为 $AC=4$,
所以
$\begin{split}FC\left(AC+EC\right)& =\dfrac{4}{x+1}\left[4+2\left(x-1\right)\right]\\ &=\dfrac{4}{x+1}\cdot2\left(x+1\right)\\ &=8.\end{split}$
所以 $FC\left(AC+EC\right)$ 的值为定值.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3