如图,折叠矩形 $OABC $ 的一边 $BC$,使点 $C$ 落在 $OA$ 边的点 $D$ 处,已知折痕 $ BE=5\sqrt 5$,且 $\dfrac{OD}{OE}=\dfrac 43$,以 $O$ 为原点,$OA$ 所在的直线为 $x$ 轴建立如图所示的平面直角坐标系,抛物线 $l:y=-\dfrac{1}{16}x^2+\dfrac 12x+c$ 经过点 $E$,且与 $AB$ 边相交于点 $F$.若 $M$ 是 $BE$ 的中点,连接 $ MF$,求证:$MF \perp BD$.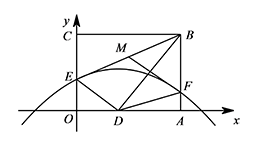
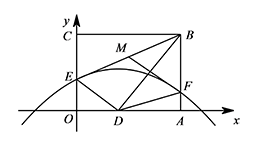
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
由折叠知 $\angle ADB=90^\circ-\angle ODE=\angle OED$,
所以 $\mathrm {Rt}\triangle ABD\backsim \mathrm {Rt}\triangle ODE.$
设 $OE=3k$,则 $OD=4k,CE=DE=5k,AB=OC=8k$.
由 $\mathrm {Rt}\triangle ABD\backsim \mathrm {Rt}\triangle ODE$ 可得 $AD=6k,OA=BC=BD=10k$,
于是 $BE=\sqrt{\left(5k\right)^2+\left(10k\right)^2}=5\sqrt 5$,解得 $k=1$.
因为抛物线 $y=-\dfrac{1}{16}x^2+\dfrac 12x+c$ 经过点 $E\left(0,3\right)$,
所以 $c=3$.
将点 $A$ 的横坐标 $x=10$ 代入 $y=-\dfrac{1}{16}x^2+\dfrac 12x+3$,求得点 $F$ 的坐标为 $\left(10,\dfrac 74\right)$,
所以 $DF=\sqrt{AD^2+AF^2}=\sqrt{6^2+\left(\dfrac 74\right)^2}=\dfrac{25}{4}$,$BF=AB-AF=8-\dfrac 74=\dfrac{25}{4}$.
所以 $DF=BF$.
因为 $\angle BDE=90^\circ$,$M$ 是 $BE$ 的中点,
所以 $ MB=MD$.
所以 $MF$ 是线段 $BD$ 的中垂线,故 $MF\perp BD$.
所以 $\mathrm {Rt}\triangle ABD\backsim \mathrm {Rt}\triangle ODE.$
设 $OE=3k$,则 $OD=4k,CE=DE=5k,AB=OC=8k$.
由 $\mathrm {Rt}\triangle ABD\backsim \mathrm {Rt}\triangle ODE$ 可得 $AD=6k,OA=BC=BD=10k$,
于是 $BE=\sqrt{\left(5k\right)^2+\left(10k\right)^2}=5\sqrt 5$,解得 $k=1$.
因为抛物线 $y=-\dfrac{1}{16}x^2+\dfrac 12x+c$ 经过点 $E\left(0,3\right)$,
所以 $c=3$.
将点 $A$ 的横坐标 $x=10$ 代入 $y=-\dfrac{1}{16}x^2+\dfrac 12x+3$,求得点 $F$ 的坐标为 $\left(10,\dfrac 74\right)$,
所以 $DF=\sqrt{AD^2+AF^2}=\sqrt{6^2+\left(\dfrac 74\right)^2}=\dfrac{25}{4}$,$BF=AB-AF=8-\dfrac 74=\dfrac{25}{4}$.
所以 $DF=BF$.
因为 $\angle BDE=90^\circ$,$M$ 是 $BE$ 的中点,
所以 $ MB=MD$.
所以 $MF$ 是线段 $BD$ 的中垂线,故 $MF\perp BD$.
答案
解析
备注