如图,抛物线 $y= -\dfrac12x^2+bx+c$ 与 $x$ 轴分别相交于点 $A\left(-2,0\right)$,$B\left(4,0\right)$,与 $y$ 轴交于点 $C$,顶点为点 $P$.动点 $ M $,$N$ 从点 $ O $ 同时出发,都以每秒 $1$ 个单位长度的速度分别在线段 $ OB $,$OC$ 上向点 $ B $,$C$ 方向运动,过点 $ M $ 作 $ x $ 轴的垂线交 $ BC $ 于点 $ F $,交抛物线于点 $ H $.是否存在这样的点 $ F $,使 $\triangle PFB$ 为直角三角形?若存在,求出点 $ F $ 的坐标;若不存在,请说明理由.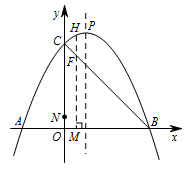

【难度】
【出处】
无
【标注】
【答案】
存在,点 $F$ 的坐标为 $\left(\dfrac 14,\dfrac {15}{4}\right)$ 或 $\left(\dfrac {1}{10},\dfrac {39}{10}\right)$
【解析】
由抛物线经过 $A\left(-2,0\right),B\left(4,0\right)$ 两点,
可得 $\begin{cases}-2-2b+c=0, \\-8+4b+c=0,\end{cases}$ 解得 $\begin{cases} b=1,\\c=4.\end{cases}$
所以抛物线的解析式为 $y=-\dfrac{1}{2}{x^2}+x+4$.
点 $C$ 的坐标为 $\left(0,4\right)$,$B\left(4,0\right)$,
① 当 $PF\perp BC$ 时.
易求直线 $BC$ 的解析式为 $y=-x+4$,可设 $PF$ 的解析式为 $y=x+m$.
代入点 $P\left(1,\dfrac 92\right)$ 坐标,得 $m=\dfrac 72$.
联立方程组 $\begin{cases} y=-x+4,\\y=x+\dfrac 72,\end{cases}$ 解得 $\begin{cases}x=\dfrac 14,\\y=\dfrac {15}{4}.\end{cases}$
所以此时点 $F$ 的坐标为 $\left(\dfrac 14,\dfrac {15}{4}\right)$;
② 当 $PF\perp BP$ 时.
易求直线 $BP$ 的解析式为 $y=-\dfrac 32x+6$,可设 $PF$ 的解析式为 $y=\dfrac 23x+n$.
代入点 $P\left(1,\dfrac 92\right)$ 坐标,得 $n=\dfrac{23}{6}$.
联立方程组 $\begin{cases}y=-x+4,\\y=\dfrac 23x+\dfrac{23}{6},\end{cases}$ 解得 $\begin{cases}x=\dfrac{1}{10},\\y=\dfrac{39}{10}.\end{cases}$
所以此时点 $F$ 的坐标为 $\left(\dfrac {1}{10},\dfrac {39}{10}\right)$.
综上所述,$\triangle PFB$ 为直角三角形时,点 $F$ 的坐标为 $\left(\dfrac 14,\dfrac {15}{4}\right)$ 或 $\left(\dfrac {1}{10},\dfrac {39}{10}\right)$.
可得 $\begin{cases}-2-2b+c=0, \\-8+4b+c=0,\end{cases}$ 解得 $\begin{cases} b=1,\\c=4.\end{cases}$
所以抛物线的解析式为 $y=-\dfrac{1}{2}{x^2}+x+4$.
点 $C$ 的坐标为 $\left(0,4\right)$,$B\left(4,0\right)$,
① 当 $PF\perp BC$ 时.
易求直线 $BC$ 的解析式为 $y=-x+4$,可设 $PF$ 的解析式为 $y=x+m$.
代入点 $P\left(1,\dfrac 92\right)$ 坐标,得 $m=\dfrac 72$.
联立方程组 $\begin{cases} y=-x+4,\\y=x+\dfrac 72,\end{cases}$ 解得 $\begin{cases}x=\dfrac 14,\\y=\dfrac {15}{4}.\end{cases}$
所以此时点 $F$ 的坐标为 $\left(\dfrac 14,\dfrac {15}{4}\right)$;
② 当 $PF\perp BP$ 时.
易求直线 $BP$ 的解析式为 $y=-\dfrac 32x+6$,可设 $PF$ 的解析式为 $y=\dfrac 23x+n$.
代入点 $P\left(1,\dfrac 92\right)$ 坐标,得 $n=\dfrac{23}{6}$.
联立方程组 $\begin{cases}y=-x+4,\\y=\dfrac 23x+\dfrac{23}{6},\end{cases}$ 解得 $\begin{cases}x=\dfrac{1}{10},\\y=\dfrac{39}{10}.\end{cases}$
所以此时点 $F$ 的坐标为 $\left(\dfrac {1}{10},\dfrac {39}{10}\right)$.
综上所述,$\triangle PFB$ 为直角三角形时,点 $F$ 的坐标为 $\left(\dfrac 14,\dfrac {15}{4}\right)$ 或 $\left(\dfrac {1}{10},\dfrac {39}{10}\right)$.
答案
解析
备注