如图，已知一条直线过点 $\left(0,4\right)$，且与抛物线 $y=\dfrac 14x^2$ 交于 $A,B$ 两点，其中点 $A$ 的横坐标是 $-2$．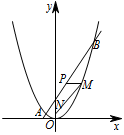
【难度】
【出处】
无
【标注】
-
在 $x$ 轴上是否存在点 $C$，使得 $\triangle ABC$ 是直角三角形？若存在，求出点 $C$ 的坐标；若不存在，请说明理由；标注答案存在，点 $C$ 的坐标为 $\left(-\dfrac12,0\right)$，$\left(0,0\right)$，$\left(6,0\right)$ 或 $\left(32,0\right)$解析因为点 $A$ 是直线与抛物线的交点，且其横坐标是 $-2$，
所以 $y=\dfrac14\times\left(-2\right)^2=1$，点 $A$ 的坐标 $\left(-2,1\right)$．
设直线 $AB$ 的函数关系式为 $y=kx+b$，则有 $\begin{cases}
b=4,\\-2k+b=1,
\end{cases}$
解得 $\begin{cases}
k=\dfrac32,\\b=4,
\end{cases}$
所以直线 $AB$ 的解析式为 $y=\dfrac32x+4$．
联立方程组 $\begin{cases}y=\dfrac 14x^2,\\ y=\dfrac 32x+4,\end{cases}$
解得 $\begin{cases}x_1=-2,\\ y_1=1,\end{cases}\begin{cases}x_2=8,\\ y_2=16.\end{cases}$
所以点 $B$ 的坐标为 $\left(8,16\right)$．
所以 $AB^2=(x_A-x_B)^2+(y_A-y_B)^2=325$．
设 $x$ 轴上的点 $C$ 坐标为 $\left(m,0\right)$，
则 $AC^2=\left(m+2\right)^2+1^2=m^2+4m+5$，$BC^2=\left(m-8\right)^2+16^2=m^2-16m+320$．
① 若 $\angle BAC=90^\circ$，则 $AB^2+AC^2=BC^2$，
即 $325+m^2+4m+5=m^2-16m+320$，
解得 $m=-\dfrac12$；
② 若 $\angle ACB=90^\circ$，则 $AB^2=AC^2+BC^2$，
即 $325=m^2+4m+5+m^2-16m+320$，
解得 $m=0$ 或 $m=6$；
③ 若 $\angle ABC=90^\circ$，则 $AB^2+BC^2= AC^2$，
即 $m^2-16m+320+ 325= m^2+4m+5$，
解得 $m=32$．
综上可得，点 $C$ 的坐标为 $\left(-\dfrac12,0\right)$，$\left(0,0\right)$，$\left(6,0\right)$ 或 $\left(32,0\right)$． -
过线段 $AB$ 上一点 $P$，作 $PM\parallel x$ 轴，交抛物线于点 $M$，点 $M$ 在第一象限，点 $N\left(0,1\right)$，当点 $M$ 的横坐标为何值时，$MN+3MP$ 的长度最大？最大值是多少？标注答案点 $M$ 的横坐标为 $6$ 时，$MN+3PM$ 的长度最大值是 $18$解析如图，令 $MP$ 与 $y$ 轴交于点 $Q$．
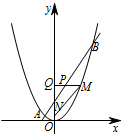设 $M\left(a,\dfrac14a^2\right)$，
则在 $\mathrm {Rt}\triangle MQN$ 中，由勾股定理得
$MN=\sqrt{a^2+\left(\dfrac14a^2-1\right)^2}=\sqrt{\dfrac{1}{16}a^4+\dfrac12a^2+1}=\dfrac14a^2+1$．
又因为点 $P$ 与点 $M$ 纵坐标相同，
所以 $\dfrac32x+4=\dfrac14a^2$，
所以 $x=\dfrac{a^2-16}{6}$，
所以点 $P$ 的横坐标为 $\dfrac{a^2-16}{6}$．
所以 $MP=a-\dfrac{a^2-16}{6}$，
所以 $MN+3PM=-\dfrac14a^2+3a+9=-\dfrac 14(a-6)^2+18$．
所以当 $a=6$ 时，$MN+3PM$ 取得最大值 $18$．
即当点 $M$ 的横坐标为 $6$ 时，$MN+3PM$ 的长度最大值是 $18$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
