如图1，平面直角坐标系中，直线 $y=-\dfrac 34x+3$ 与抛物线 $y=ax^2+\dfrac 94x+c$ 相交于 $A,B$ 两点，其中点 $A$ 在 $x$ 轴上，点 $B$ 在 $y$ 轴上．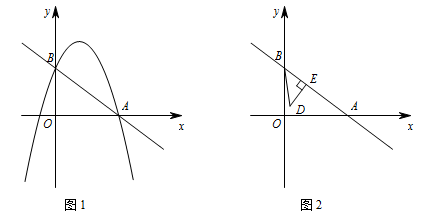
【难度】
【出处】
无
【标注】
-
在抛物线上存在一点 $M$，使 $\triangle MAB$ 是以 $AB$ 为直角边的直角三角形，求点 $M$ 的坐标；标注答案点 $M$ 的坐标为 $\left(\dfrac{11}{9},\dfrac{125}{27}\right)$ 或 $\left(-\dfrac{25}{9},-\dfrac{244}{27}\right)$解析直线 $y=-\dfrac 34x+3$ 与 $x$ 轴交于点 $A(4,0)$，与 $y$ 轴交于点 $B\left(0,3\right)$．
将 $A\left(4,0\right),B\left(0,3\right)$ 代入 $y=ax^2+\dfrac 94x+c$ 中，
得 $ \begin{cases}
16a+4\times \dfrac 94+c=0,\\
3=c,
\end{cases} $
解得 $ \begin{cases}
a=-\dfrac 34,\\
c=3.
\end{cases} $
所以抛物线的解析式为 $y=-\dfrac 34x^2+\dfrac 94x+3$．
设点 $M$ 的坐标为 $\left(x,-\dfrac 34x^2+\dfrac 94x+3\right)$．
① 当 $\angle MBA=90^\circ$ 时，作 $MN$ 垂直 $y$ 轴于点 $N$．
易证 $\triangle MNB\backsim \triangle BOA$，
所以 $\dfrac{MN}{BO}=\dfrac{BN}{AO}$，即 $\dfrac{x}{3}=\dfrac{-\dfrac 34x^2+\dfrac 94x+3-3}{4}$，
解得 $x_1=\dfrac{11}{9}$，$x_2=0$（舍去）．
所以点 $M\left(\dfrac{11}{9},\dfrac{125}{27}\right)$．
② 当 $\angle BAM=90^\circ$ 时，作 $MN$ 垂直 $x$ 轴于点 $N$．
易证 $\triangle MNA\backsim \triangle AOB$，
所以 $\dfrac{MN}{AO}=\dfrac{AN}{BO}$，即 $\dfrac{\dfrac 34x^2-\dfrac 94x-3}{4}=\dfrac{-x+4}{3}$，
解得 $x_1=-\dfrac{25}{9}$，$x_2=4$（舍去）．
所以点 $M\left(-\dfrac{25}{9},-\dfrac{244}{27}\right)$．
综上可得，满足条件的点 $M$ 的坐标为 $\left(\dfrac{11}{9},\dfrac{125}{27}\right)$ 或 $\left(-\dfrac{25}{9},-\dfrac{244}{27}\right)$． -
如图 2，点 $E$ 为线段 $AB$ 上一点，$BE=2$，以 $BE$ 为腰作等腰 $\mathrm {Rt}\triangle BDE$，使它与 $\triangle AOB$ 在直线 $AB$ 的同侧，$\angle BED=90^\circ$，$\triangle BDE$ 沿着 $BA$ 方向以每秒一个单位的速度运动，当点 $B$ 与 $A$ 重合时停止运动．设运动时间为 $t$ 秒，$\triangle BDE$ 与 $\triangle AOB$ 重叠部分的面积为 $S$．直接写出 $S$ 关于 $t$ 的函数关系式，并写出自变量 $t$ 的取值范围．标注答案$S=\begin{cases}2,&\left(0\leqslant t\leqslant \dfrac 13\right)\\
-\dfrac{9}{56}t^2+\dfrac{3}{28}t+\dfrac{111}{56},&\left(\dfrac 13<t\leqslant 3\right)\\
\dfrac{3}{14}t^2-\dfrac{15}{7}t+\dfrac{75}{14}.&\left(3<t\leqslant 5\right)\end{cases}$解析设 $\triangle B'D'E'$ 为 $\triangle BDE$ 移动后对应的图形．
当点 $D'$ 在 $AO$ 上时，如图所示．
易得 $\dfrac{D'E'}{AE'}=\dfrac{BO}{AO}$，即 $\dfrac{2}{AE'}=\dfrac 34$，
所以 $AE'=\dfrac 83$，$BE'=5-\dfrac 83=\dfrac 73$，$BB'=\dfrac 13$，
此时 $t=\dfrac 13$；
当点 $E'$ 与点 $A$ 重合时，$BB'=AB-B'E=3$，所以 $t=3$；
当点 $B'$ 与点 $A$ 重合时，$BB'=AB=5$，所以 $t=5$．
① 当 $0\leqslant t\leqslant \dfrac 13$ 时，$S=S_{\triangle B'E'D'}=2$；
② 当 $\dfrac 13<t\leqslant 3$ 时，$BB'=t$，$AB'=5-t$，$AE'=3-t$．
如图，记 $B'D',E'D'$ 与 $OA$ 的交点为点 $F,G$．
易得 $E'G=\dfrac 34AE'=\dfrac{9-3t}4$，
所以 $D'G=2-\dfrac{9-3t}4=\dfrac{3t-1}4$．
过点 $F$ 作 $FH\perp D'E'$ 于点 $H$，则 $D'H=FH$，$GH=\dfrac 34FH$，
所以 $D'G=\dfrac 74FH$，即 $\dfrac{3t-1}4=\dfrac 74FH$，
所以 $FH=\dfrac{3t-1}7$．
从而 $S=S_{\triangle B'E'D'}-S_{\triangle FGD'}=2-\dfrac 12\times\dfrac{3t-1}7\times\dfrac{3t-1}4=-\dfrac{9}{56}t^2+\dfrac{3}{28}t+\dfrac{111}{56}$；
③ 当 $3<t\leqslant 5$ 时，$BB'=t$，$AB'=5-t$．
如图，记 $B'D'$ 与 $OA$ 的交点为 $F$，过点 $F$ 作 $FG\perp AB$ 于点 $G$．
易得 $B'G=FG$，$AG=\dfrac 43FG$，
所以 $AB'=\dfrac 73FG$，即 $5-t=\dfrac 73FG$，
所以 $FG=\dfrac{15-3t}7$．
从而 $S=S_{\triangle FAB'}=\dfrac 12\times \dfrac{15-3t}7\times(5-t)=\dfrac{3}{14}t^2-\dfrac{15}{7}t+\dfrac{75}{14}$．
综上可得，$S=\begin{cases}2,&\left(0\leqslant t\leqslant \dfrac 13\right)\\
-\dfrac{9}{56}t^2+\dfrac{3}{28}t+\dfrac{111}{56},&\left(\dfrac 13<t\leqslant 3\right)\\
\dfrac{3}{14}t^2-\dfrac{15}{7}t+\dfrac{75}{14}.&\left(3<t\leqslant 5\right)\end{cases}$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
