如图，在平面直角坐标系 $xOy$ 中，抛物线 $y=x^2-2x-3$ 交 $x$ 轴于 $A,B$ 两点，交 $y$ 轴于点 $C$，直线 $y=x-3$ 经过 $B,C$ 两点，过点 $C$ 作直线 $CD\perp y$ 轴交抛物线与另一点 $D$，点 $P$ 是直线 $CD$ 下方抛物线上的一个动点，且抛物线对称轴的右侧，过点 $P$ 作 $PE\perp x$ 轴于点 $E$，$PE$ 交 $CD$ 于点 $F$，交 $BC$ 于点 $M$，连接 $AC$，过点 $M$ 作 $MN\perp AC$ 于点 $N$，设点 $P$ 的横坐标为 $t$，线段 $MN$ 的长为 $d$，求 $d$ 与 $t$ 之间的函数关系式（不要求写出自变量 $t$ 的取值范围）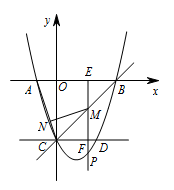
【难度】
【出处】
无
【标注】
【答案】
$d=\dfrac{2\sqrt{10}}{5}t$
【解析】
由题意可得 $A(-1,0),B(3,0),C(0,-3)$，
所以 $\angle ABC=45^\circ$，$AC=\sqrt{10}$，$AB=4$，
所以 $\angle EMB=\angle EBM=45^\circ$．
因为 $P$ 的横坐标为 $t$，
所以 $EM=EB=3-t$．
连接 $AM$，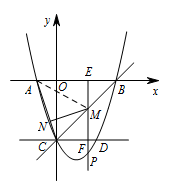
因为 $S_{\triangle ABC}=S_{\triangle AMC}+S_{\triangle AMB}$，
所以 $\dfrac 12AB\cdot OC=\dfrac 12AC\cdot MN+\dfrac 12AB\cdot EM$，
所以 $\dfrac 12\times 4\times 3=\dfrac 12\times \sqrt{10}d+\dfrac 12\times 4(3-t)$，
所以 $d=\dfrac{2\sqrt{10}}{5}t$．
所以 $\angle ABC=45^\circ$，$AC=\sqrt{10}$，$AB=4$，
所以 $\angle EMB=\angle EBM=45^\circ$．
因为 $P$ 的横坐标为 $t$，
所以 $EM=EB=3-t$．
连接 $AM$，
因为 $S_{\triangle ABC}=S_{\triangle AMC}+S_{\triangle AMB}$，所以 $\dfrac 12AB\cdot OC=\dfrac 12AC\cdot MN+\dfrac 12AB\cdot EM$，
所以 $\dfrac 12\times 4\times 3=\dfrac 12\times \sqrt{10}d+\dfrac 12\times 4(3-t)$，
所以 $d=\dfrac{2\sqrt{10}}{5}t$．
答案
解析
备注
