如图，已知抛物线 $y=ax^2+bx+c$（$a\neq 0$）经过点 $A\left(-3,2\right)$，$B\left(0,-2\right)$，其对称轴为直线 $x=\dfrac52$，$C\left(0,\dfrac12\right)$ 为 $y$ 轴上一点，直线 $AC$ 与抛物线交于另一点 $D$．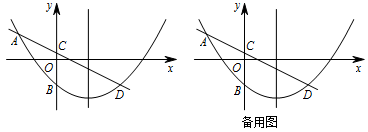
【难度】
【出处】
无
【标注】
-
试在线段 $AD$ 下方的抛物线上求一点 $E$，使得 $\triangle ADE$ 的面积最大，并求出最大面积；标注答案点 $E$ 坐标为 $\left(1,- \dfrac83\right)$ 时，$\triangle ADE$ 的面积最大，最大面积为 $\dfrac{32}3$解析根据题意得 $ \begin{cases}9a-3b+c=2,\\c=-2,\\-\dfrac{b}{2a}=\dfrac52,\end{cases} $
解得 $ \begin{cases}a=\dfrac16,\\b=-\dfrac{5}{6},\\c=-2.\end{cases} $
所以抛物线解析式为 $y= \dfrac16x^2- \dfrac56x-2$．
作 $EP\parallel y$ 轴交 $AD$ 于 $P$，如图，
设直线 $AD$ 的解析式为 $y=mx+n$，
把 $A\left(-3,2\right)$，$C\left(0, \dfrac12\right)$ 分别代入得 $ \begin{cases}-3m+n=2,\\n=\dfrac12,\end{cases} $
解得 $ \begin{cases}m=-\dfrac12,\\n=\dfrac12\end{cases} $
所以直线 $AD$ 的解析式为 $y=-\dfrac12 x+\dfrac12$．
解方程组 $ \begin{cases}y=\dfrac16x^2-\dfrac56x-2,\\y=-\dfrac12x+\dfrac12,\end{cases} $
得 $ \begin{cases}x=-3,\\y=2\end{cases} 或 \begin{cases}x=5,\\y=-2.\end{cases} $
则 $D\left(5,-2\right)$．
设 $E\left(x, \dfrac16x^2- \dfrac56x-2\right)$（$-3<x<5$），
则 $P\left(x,- \dfrac12x+ \dfrac12\right)$，
所以 $PE=- \dfrac12x+\dfrac12 -\left(\dfrac16 x^2-\dfrac56 x-2\right)=-\dfrac16 x^2+ \dfrac13x+\dfrac52$，
$\begin{split}\text{从而}S_{\triangle AED}&=S_{\triangle AEP}+S_{\triangle DEP}
\\ &= \dfrac12\cdot \left(5+3\right)\cdot \left(-\dfrac16 x^2+ \dfrac13x+ \dfrac52\right)
\\ &=-\dfrac23 \left(x-1\right)^2+ \dfrac{32}{3},\end{split} $
当 $x=1$ 时，$\triangle ADE$ 的面积最大，最大面积为 $\dfrac{32}3$，此时 $E$ 点坐标为 $\left(1,- \dfrac83\right)$． -
在抛物线的对称轴上是否存在一点 $F$，使得 $\triangle ADF$ 是直角三角形？如果存在，求点 $F$ 的坐标；如果不存在，请说明理由．标注答案存在，点 $F$ 的坐标为 $\left(\dfrac52,13\right)$，$\left(\dfrac52,-7\right)$，$\left(\dfrac52,\dfrac{\sqrt{71}}2\right)$ 或 $\left(\dfrac52,-\dfrac{\sqrt{71}}2\right)$解析由 $A\left(-3,2\right),D\left(5,-2\right)$，可得 $AD^2=\left(5+3\right)^2+\left(-2-2\right)^2=80$．
设点 $F$ 的坐标为 $\left(\dfrac52,t\right)$，
则 $AF^2=\left(\dfrac52+3\right)^2+\left(t-2\right)^2$，$DF^2=\left(5-\dfrac52\right)^2+\left(-t-2\right)^2$．
① 若 $\angle DAF=90^\circ$，则 $AD^2+AF^2=DF^2$，
所以 $80+\left(\dfrac52+3\right)^2+\left(t-2\right)^2=\left(5-\dfrac52\right)^2+\left(-t-2\right)^2$，
解得 $t=13$，此时 $F$ 点坐标为 $\left(\dfrac52,13\right)$；
② 若 $\angle ADF=90^\circ$，则 $AD^2+DF^2=AF^2$，
所以 $80+\left(5-\dfrac52\right)^2+\left(-t-2\right)^2=\left(\dfrac52+3\right)^2+\left(t-2\right)^2$，
解得 $t=-7$，此时 $F$ 点坐标为 $\left(\dfrac52,-7\right)$；
③ 若 $\angle AFD=90^\circ$，则 $DF^2+AF^2=AD^2$，
所以 $\left(\dfrac52+3\right)^2+\left(t-2\right)^2+\left(5-\dfrac52\right)^2+\left(-t-2\right)^2=80$，
解得 $t=\pm\dfrac{\sqrt{71}}2 $，此时 $F$ 点坐标为 $\left(\dfrac52,\dfrac{\sqrt{71}}2\right)$ 或 $\left(\dfrac52,-\dfrac{\sqrt{71}}2\right)$．
综上所述，点 $F$ 的坐标为 $\left(\dfrac52,13\right)$ 或 $\left(\dfrac52,-7\right)$ 或 $\left(\dfrac52,\dfrac{\sqrt{71}}2\right)$ 或 $\left(\dfrac52,-\dfrac{\sqrt{71}}2\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
