如图，点 $P$ 在双曲线 $y= \dfrac 1x\left(x>0\right)$ 上，点 $M$ 在直线 $l:y=-x+\sqrt 2$ 上，且 $PM\parallel x$ 轴．若点 $N$ 的坐标为 $\left(0,2\sqrt2 \right)$，求 $PM+PN$ 最小值以及此时点 $P$ 的坐标．
【难度】
【出处】
无
【标注】
【答案】
$PM+PN$ 取最小值 $2$ 时，点 $P$ 的坐标为 $\left( \sqrt 2-1,\sqrt 2 +1\right)$
【解析】
设点 $M$ 的坐标为 $(-m+\sqrt 2,m)$，则点 $P$ 的坐标为 $\left(\dfrac 1m,m\right)$．
$\begin{split}PM&=x_P-x_M=\dfrac 1m-(-m+\sqrt 2)\\ &=\sqrt{ \left(m+\dfrac 1m-\sqrt 2 \right)^2}\\ &=\sqrt{\left(m+\dfrac 1m\right)^2-2\sqrt 2 \left(m+\dfrac 1m\right)+2}\\&=\sqrt{\left(\dfrac 1{m^2}-\dfrac{2\sqrt 2}m+2\right)+\left(m^2-2\sqrt 2m+2\right)}\\&=\sqrt{\left(\dfrac 1m-\sqrt 2\right)^2+\left(m-\sqrt 2\right)^2}.\end{split}$
记坐标为 $(\sqrt 2,\sqrt 2)$ 点为 $F$，则 $PM=PF$，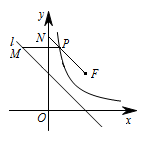
所以 $(PM+PN)_{最小}=(PF+PN)_{最小}=FN=2$．
此时点 $P$ 为线段 $NF$ 与双曲线的交点．
由 $N,F$ 两点的坐标可得直线 $NF$ 解析式为 $y=-x+2\sqrt 2$，
联立方程组 $\begin{cases}y=-x+2\sqrt 2,\\ y=\dfrac 1x,\end{cases}$
解得 $\begin{cases}x_1=\sqrt 2 -1,\\y_1=\sqrt 2+1,\end{cases}\begin{cases}x_2=\sqrt 2+1,\\y_2=\sqrt 2-1.\end{cases}$
因为点 $P$ 在线段 $NF$ 上，
所以 $PM+PN$ 取最小值 $2$ 时，点 $P$ 的坐标为 $\left( \sqrt 2-1,\sqrt 2 +1\right)$．
$\begin{split}PM&=x_P-x_M=\dfrac 1m-(-m+\sqrt 2)\\ &=\sqrt{ \left(m+\dfrac 1m-\sqrt 2 \right)^2}\\ &=\sqrt{\left(m+\dfrac 1m\right)^2-2\sqrt 2 \left(m+\dfrac 1m\right)+2}\\&=\sqrt{\left(\dfrac 1{m^2}-\dfrac{2\sqrt 2}m+2\right)+\left(m^2-2\sqrt 2m+2\right)}\\&=\sqrt{\left(\dfrac 1m-\sqrt 2\right)^2+\left(m-\sqrt 2\right)^2}.\end{split}$
记坐标为 $(\sqrt 2,\sqrt 2)$ 点为 $F$，则 $PM=PF$，
所以 $(PM+PN)_{最小}=(PF+PN)_{最小}=FN=2$．此时点 $P$ 为线段 $NF$ 与双曲线的交点．
由 $N,F$ 两点的坐标可得直线 $NF$ 解析式为 $y=-x+2\sqrt 2$，
联立方程组 $\begin{cases}y=-x+2\sqrt 2,\\ y=\dfrac 1x,\end{cases}$
解得 $\begin{cases}x_1=\sqrt 2 -1,\\y_1=\sqrt 2+1,\end{cases}\begin{cases}x_2=\sqrt 2+1,\\y_2=\sqrt 2-1.\end{cases}$
因为点 $P$ 在线段 $NF$ 上，
所以 $PM+PN$ 取最小值 $2$ 时，点 $P$ 的坐标为 $\left( \sqrt 2-1,\sqrt 2 +1\right)$．
答案
解析
备注
