如图，在平面直角坐标系 $xOy$ 中，点 $A$ 的坐标是 $(-4,0)$，点 $B$ 的坐标是 $(0,b)$（$b>0$）．$P$ 是直线 $AB$ 上的一个动点，作 $PC\perp x$ 轴，垂足为点 $C$．记点 $P$ 关于 $y$ 轴的对称点为 $P'$（点 $P'$ 不在 $y$ 轴上），连接 $PP',P'A,P'C$．设点 $P$ 的横坐标为 $a$．问是否同时存在 $a,b$，使得 $\triangle P'CA$ 为等腰直角三角形？若存在，请求出所有满足要求的 $a,b$ 的值；若不存在，请说明理由．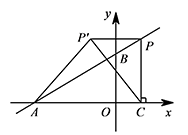
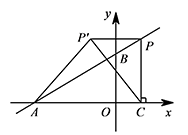
【难度】
【出处】
无
【标注】
【答案】
存在，$a=\dfrac 43,b=2$ 或 $a=b=4$
【解析】
以下分三种情况讨论．
① 当点 $P$ 在第一象限时，
（i）若 $\angle AP'C=90^\circ$，$P'A=P'C$，如图．
过点 $P'$ 作 $P'H\perp x$ 轴于点 $H$．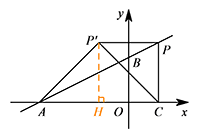
此时 $\triangle AP'C$ 为等腰直角三角形，$CH=AH$．
由题意可得 $OC=OH=a$，从而 $CH=2a$，$HA=4-a$，
所以 $-a+4=2a$，
解得 $a=\dfrac 43$．
此时 $P'H=CH=\dfrac 83$，
则点 $P$ 的坐标为 $(\dfrac 43,\dfrac 83)$．
所以直线 $AP$ 的解析式为 $y=\dfrac 12x+2$，从而 $b=2$．
（ii）若 $\angle P'AC=90^\circ$，$P'A=CA$，如图．
此时四边形 $P'ACP$ 为正方形，
所以 $a=OA=4$，$b=OB=4$．
（iii）若 $\angle P'CA=90^\circ$，点 $P,P'$ 在 $y$ 轴上重合，不符合题意．
② 当点 $P$ 在第二象限时，$\angle P'CA$ 为钝角，如图．
则 $\triangle P'CA$ 不可能是等腰直角三角形．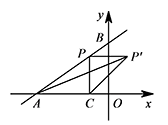
③ 当点 $P$ 在第三象限时，$\angle P'AC$ 为钝角，如图．
则 $\triangle P'CA$ 不可能是等腰直角三角形．
综上所得，符合要求的 $a,b$ 为 $a=\dfrac 43,b=2$ 或 $a=b=4$．
① 当点 $P$ 在第一象限时，
（i）若 $\angle AP'C=90^\circ$，$P'A=P'C$，如图．
过点 $P'$ 作 $P'H\perp x$ 轴于点 $H$．
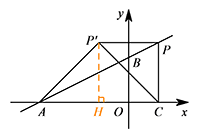此时 $\triangle AP'C$ 为等腰直角三角形，$CH=AH$．由题意可得 $OC=OH=a$，从而 $CH=2a$，$HA=4-a$，
所以 $-a+4=2a$，
解得 $a=\dfrac 43$．
此时 $P'H=CH=\dfrac 83$，
则点 $P$ 的坐标为 $(\dfrac 43,\dfrac 83)$．
所以直线 $AP$ 的解析式为 $y=\dfrac 12x+2$，从而 $b=2$．
（ii）若 $\angle P'AC=90^\circ$，$P'A=CA$，如图．
此时四边形 $P'ACP$ 为正方形，所以 $a=OA=4$，$b=OB=4$．
（iii）若 $\angle P'CA=90^\circ$，点 $P,P'$ 在 $y$ 轴上重合，不符合题意．
② 当点 $P$ 在第二象限时，$\angle P'CA$ 为钝角，如图．
则 $\triangle P'CA$ 不可能是等腰直角三角形．
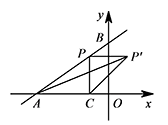③ 当点 $P$ 在第三象限时，$\angle P'AC$ 为钝角，如图．则 $\triangle P'CA$ 不可能是等腰直角三角形．
综上所得，符合要求的 $a,b$ 为 $a=\dfrac 43,b=2$ 或 $a=b=4$．
答案
解析
备注
