如图，边长为 $8$ 的正方形 $OABC$ 的两边在坐标轴上，以点 $C$ 为顶点的抛物线经过点 $A$，点 $P$ 是抛物线上点 $A,C$ 间的一个动点（含端点），过点 $P$ 作 $PF\perp BC$ 于点 $F$．点 $D,E$ 的坐标分别为 $\left(0,6\right),\left(-4,0\right)$，连接 $PD,PE,DE$．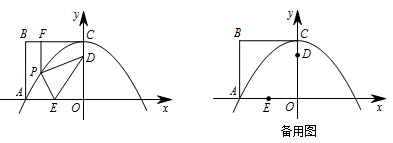
【难度】
【出处】
无
【标注】
-
小明探究点 $P$ 的位置发现：当点 $P$ 与点 $A$ 或点 $C$ 重合时，$PD$ 与 $PF$ 的差为定值．进而猜想：对于任意一点 $P$，$PD$ 与 $PF$ 的差为定值．请你判断该猜想是否正确，并说明理由；标注答案正确解析由题意得点 $A,B,C$ 的坐标分别为 $(-8,0),(-8,8),(0,8)$．
可设抛物线的解析式为 $y=ax^2+8$，
将点 $A$ 坐标代入，得 $a=-\dfrac 18$．
所以抛物线的解析式为 $y=-\dfrac 18x^2+8$．
设点 $P$ 的坐标为 $\left(x,-\dfrac 18x^2+8\right)$，则 $PF=8-\left(-\dfrac 18x^2+8\right)=\dfrac 18x^2$．
过点 $P$ 作 $PM\perp y$ 轴于点 $M$．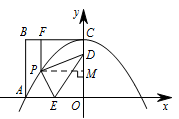
则 $PD=\sqrt{PM^2+DM^2}=\sqrt{\left(\dfrac 18x^2+2\right)^2}=\dfrac 18x^2+2$．
所以 $PD-PF=\dfrac 18x^2+2-\dfrac 18x^2=2$．
故猜想正确． -
小明进一步探究得出结论：若将"使 $\triangle PDE$ 的面积为整数"的点 $P$ 记作"好点"，则存在多个"好点"，且使 $\triangle PDE$ 的周长最小的点 $P$ 也是一个"好点"．请直接写出所有"好点"的个数，并求出 $\triangle PDE$ 周长最小时"好点"的坐标．标注答案"好点"共有 $11$ 个解析在点 $P$ 运动时，$DE$ 大小不变，
所以 $ PE$ 与 $PD$ 的和最小时，$\triangle PDE$ 的周长最小．
因为 $PD-PF=2$，
所以 $ PD=PF+2$．
所以 $PE+PD=PE+PF+2$．
当 $P,E,F$ 三点共线时，$PE+PF$ 最小．
此时点 $P$ 的横坐标都为 $-4$．
将 $x=-4$ 代入 $y=-\dfrac 18x^2+8$，得 $y=6$．
所以 $ P\left(-4,6\right)$，此时 $\triangle PDE$ 的周长最小，且 $\triangle PDE$ 的面积为 $12$，点 $P$ 恰为"好点"．
所以 $ \triangle PDE$ 的周长最小时"好点"的坐标为 $\left(-4,6\right)$ $\triangle PDE$ 的面积 $S=-\dfrac 14x^2-3x+4=-\dfrac 14\left(x+6\right)^2+13$．
由 $-8\leqslant x\leqslant 0$，知 $4\leqslant S\leqslant 13$，
所以 $S$ 的整数值有 $10$ 个．
由函数图象知，当 $S=12$ 时，对应的"好点"有 $2$ 个．
所以"好点"共有 $11$ 个．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
