在平面直角坐标系 $xOy$ 中，$\triangle ABC$ 的顶点坐标分别是 $A(x_1,y_1),B(x_2,y_2),C(x_3,y_3)$，对于 $\triangle ABC$ 的横长、纵长、纵横比给出如下定义：
将 $|x_1-x_2|,|x_2-x_3|,|x_3-x_1|$ 中的最大值，称为 $\triangle ABC$ 的横长，记作 $D_x$；将 $|y_1-y_2|,|y_2-y_3|,|y_3-y_1|$ 中的最大值，称为 $\triangle ABC$ 的纵长，记作 $D_y$；将 $\dfrac{D_y}{D_x}$ 叫做 $\triangle ABC$ 的纵横比，记作 $\lambda=\dfrac{D_y}{D_x}$．
如图，若点 $A$ 的坐标为 $(1,0)$．
将 $|x_1-x_2|,|x_2-x_3|,|x_3-x_1|$ 中的最大值，称为 $\triangle ABC$ 的横长，记作 $D_x$；将 $|y_1-y_2|,|y_2-y_3|,|y_3-y_1|$ 中的最大值，称为 $\triangle ABC$ 的纵长，记作 $D_y$；将 $\dfrac{D_y}{D_x}$ 叫做 $\triangle ABC$ 的纵横比，记作 $\lambda=\dfrac{D_y}{D_x}$．
如图，若点 $A$ 的坐标为 $(1,0)$．
【难度】
【出处】
无
【标注】
-
点 $B$ 在第四象限，若 $\triangle AOB$ 的横纵比 $1$，写出一个符合条件的点 $B$ 的坐标；标注答案$B(1,-1)$解析略
-
如图1，点 $C$ 是双曲线 $y=\dfrac 1{2x}$ 上一个动点，若 $\triangle AOC$ 的纵横比为 $1$，求点 $C$ 的坐标；标注答案点 $C$ 的坐标为 $\left(\dfrac 12,1\right)$ 或 $\left(\dfrac{1-\sqrt 3}2,-\dfrac{1+\sqrt 3}2\right)$解析如图，设点 $C$ 的坐标为 $\left(c,\dfrac 1{2c}\right)$，则 $D_y=\left|\dfrac 1{2c}\right|$．
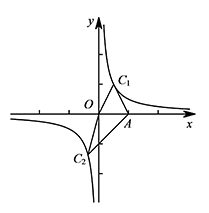① 如图，当点 $C$ 在第一象限时，$D_y=\dfrac 1{2c}$．
i）若 $0<c\leqslant 1$，则 $D_x=1$，此时 $\lambda=\dfrac{D_y}{D_x}=\dfrac 1{2c}=1$，
解得 $c=\dfrac 12$．
所以点 $C$ 的坐标为 $C_1\left(\dfrac 12,1\right)$；
ii）若 $c>1$，则 $D_x=c$，此时 $\lambda=\dfrac{D_y}{D_x}=\dfrac{\dfrac 1{2c}}{c}=1$，
解得 $c=\pm\dfrac{\sqrt 2}2<1$，故舍去．
② 如图，当点 $C$ 在第三象限时，$D_x=1-c$，$D_y=-\dfrac 1{2c}$．
此时 $\lambda=\dfrac{D_y}{D_x}=\dfrac{-\dfrac 1{2c}}{1-c}=1$，
解得 $c_1=\dfrac{1-\sqrt 3}2$，$c_2=\dfrac{1+\sqrt 3}2$（舍去）．
所以点 $C$ 的坐标为 $C_2\left(\dfrac{1-\sqrt 3}2,-\dfrac{1+\sqrt 3}2\right)$．
综上所述，满足题意的点 $C$ 的坐标为 $\left(\dfrac 12,1\right)$ 或 $\left(\dfrac{1-\sqrt 3}2,-\dfrac{1+\sqrt 3}2\right)$． -
如图2，$\odot P$ 以 $P(0,\sqrt 3)$ 为圆心，$1$ 为半径，点 $D$ 是 $\odot P$ 上一个动点，直接写出 $\triangle AOD$ 的纵横比 $\lambda$ 的取值范围．标注答案$\dfrac{\sqrt 3}3\leqslant \lambda\leqslant 1+\sqrt 3$解析设点 $D$ 的坐标为 $\left(m,n\right)$，则 $n\leqslant 1+\sqrt 3$．
① 若 $0\leqslant d\leqslant 1$，则 $D_x=1$．
所以 $\lambda=\dfrac{D_y}{D_x}=n\leqslant 1+\sqrt 3$；
② 若 $-1\leqslant d<0$，过点 $D$ 作 $DE\perp x$ 轴于点 $E$．
此时 $\lambda=\dfrac{D_y}{D_x}=\dfrac{DE}{AE}=\tan \angle DAE$．
如图，当 $AD$ 与 $\odot P$ 相切时，$\lambda$ 取最小值．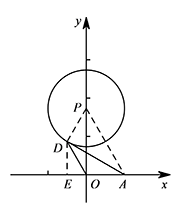
连接 $AP,DP$，则 $AP=\sqrt{AD^2+PD^2}=2$，
所以 $\sin \angle PAO=\dfrac{OP}{AP}=\dfrac{\sqrt 3}{2}$，$\sin \angle PAD=\dfrac{DP}{PA}=\dfrac 12$，
所以 $\angle PAO=60^\circ$，$\angle PAD=30^\circ$，
所以 $\angle DAE=30^\circ$，即 ${\lambda}_{最小}=\dfrac{\sqrt 3}{3}$．
综上所述，$\triangle AOD$ 的纵横比 $\lambda$ 的取值范围为 $\dfrac{\sqrt 3}3\leqslant \lambda\leqslant 1+\sqrt 3$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
