抛物线 $y=ax^2+bx+4$（$a\neq 0$）过点 $A\left(1,-1\right)$，$B\left(5,-1\right)$，与 $y$ 轴交于点 $C$．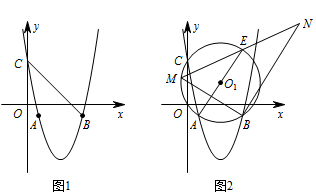
【难度】
【出处】
无
【标注】
-
如图 1，连接 $CB$，以 $CB$ 为边作平行四边形 $CBPQ$，若点 $P$ 在直线 $BC$ 上方的抛物线上，$Q$ 为坐标平面内的一点，且平行四边形 $CBPQ$ 的面积为 $30$，求点 $P$ 的坐标；标注答案点 $P$ 的坐标为 $\left(6,4\right)$解析将点 $A$，$B$ 的坐标代入抛物线的解析式，
得 $ \begin{cases}a+b+4=-1,\\25a+5b+4=-1,\end{cases} $
解得 $ \begin{cases}a=1,\\b=-6.\end{cases} $
所以抛物线得解析式为 $y=x^2-6x+4$．
如图所示：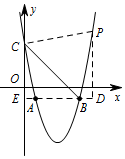
设点 $P$ 的坐标为 $P\left(m,m^2-6m+4\right)$，
因为平行四边形的面积为 $30$，
所以 $ S_{\triangle CBP}=15$，
即 $S_{\triangle CBP}=S_{梯形CEDP}-S_{\triangle CEB}-S_{\triangle PBD}$．
所以 $ \dfrac12m\left(5+m^2-6m+4+1\right)- \dfrac12\times 5\times 5- \dfrac12\left(m-5\right)\left(m^2-6m+5\right)=15$．
化简得 $m^2-5m-6=0$，
解得 $m=6$，或 $m=-1$．
因为 $m>0$，
所以 点 $P$ 的坐标为 $\left(6,4\right)$． -
如图 2，$\odot O_{1}$ 过点 $A$，$B$，$C$ 三点，$AE$ 为直径，点 $M$ 为 $\overparen{ACE}$ 上的一动点（不与点 $A$，$E$ 重合），$\angle MBN$ 为直角，边 $BN$ 与 $ME$ 的延长线交于 $N$，求线段 $BN$ 长度的最大值．标注答案$ 3\sqrt{13}$解析
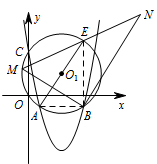连接 $AB$，$EB$．
因为 $ AE$ 是圆的直径，
所以 $ \angle ABE=90^\circ $，
所以 $ \angle ABE=\angle MBN$．
因为 $\angle EAB=\angle EMB$，
所以 $ \triangle EAB\backsim \triangle NMB$．
因为 $A\left(1,-1\right)$，$B\left(5,-1\right)$，
所以点 $O_1$ 的横坐标为 $3$．
将 $x=0$ 代入抛物线的解析式得 $y=4$，
所以点 $C$ 的坐标为 $\left(0,4\right)$．
设点 $O_1$ 的坐标为 $\left(3,m\right)$，
因为 $ O_1C=O_1A$，
所以 $\sqrt{3^2+\left(m-4\right)^2}=\sqrt{2^2+\left(m+1\right)^2} $，
解得 $m=2$，
所以点 $O_1$ 的坐标为 $\left(3,2\right)$，
所以 $ O_1A=\sqrt{3^2+\left(2-4\right)^2}=\sqrt{13} $．
在 $\mathrm {Rt}\triangle ABE$ 中，
由勾股定理得
$BE=\sqrt{AE^2-AB^2} =\sqrt{\left(2\sqrt{13}\right)^2-4^2} =6$，
所以点 $E$ 的坐标为 $\left(5,5\right)$，
所以 $AB=4$，$BE=6$．
因为 $\triangle EAB\backsim \triangle NMB$，
所以 $\dfrac{AB}{EB}=\dfrac{MB}{NB} $，
所以 $ \dfrac46=\dfrac{MB}{NB}$．
所以 $ NB=\dfrac32MB $，
所以当 $MB$ 为直径时，$MB$ 最大，此时 $NB$ 最大，
所以 $ MB=AE=2\sqrt{13}$，
所以 $ NB=\dfrac32\times2\sqrt{13} =3\sqrt{13}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
