如图，已知点 $A$ 的坐标为 $\left(-2,0\right)$，直线 $y=-\dfrac{3}{4}x+3$ 与 $x$ 轴，$y$ 轴分别交于点 $B$ 和点 $C$，连接 $AC$，顶点为 $D$ 的抛物线 $y=ax^{2}+bx+c$ 过 $A,B,C$ 三点．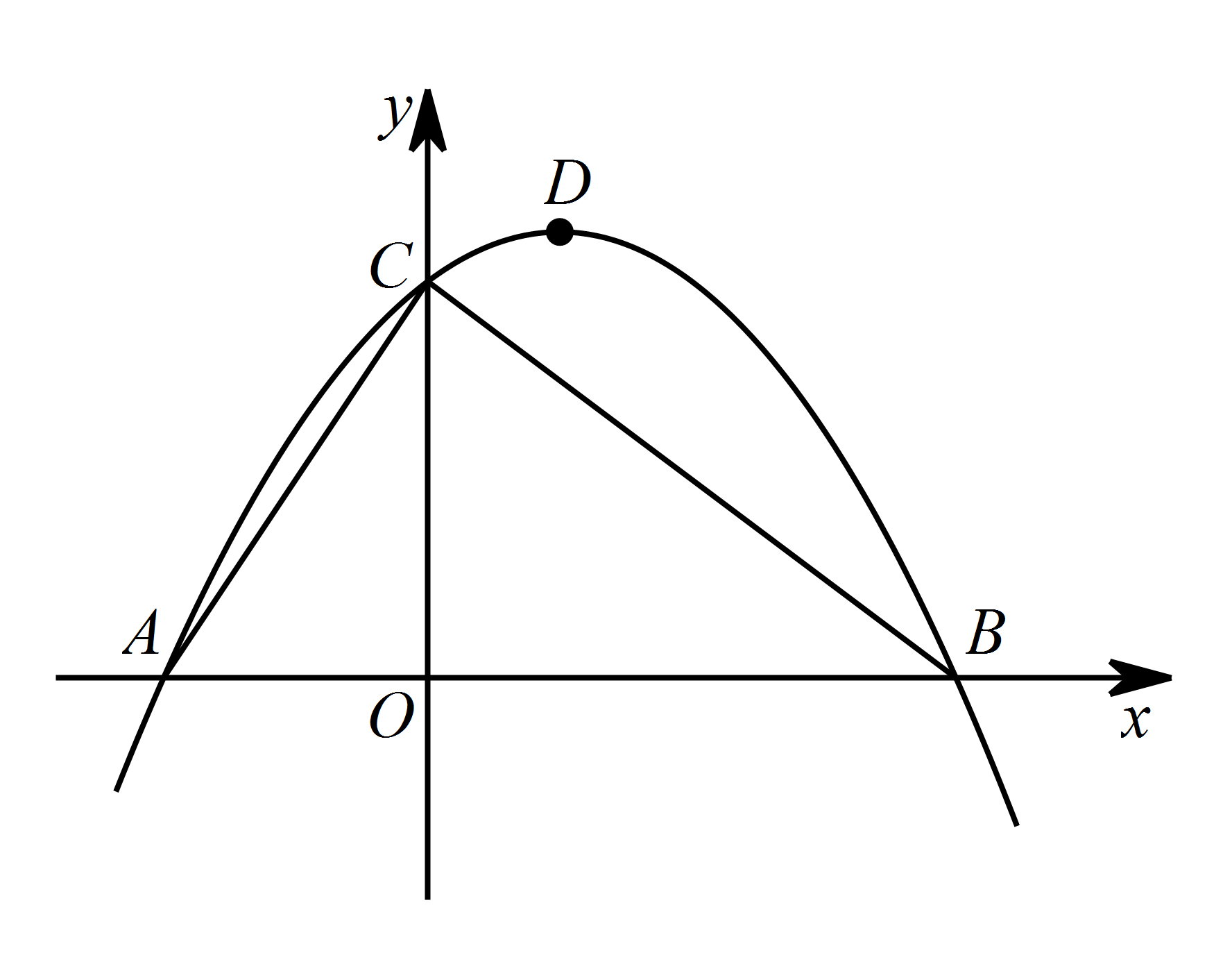
【难度】
【出处】
无
【标注】
-
设抛物线的对称轴 $DE$ 交线段 $BC$ 于点 $E,P$ 是第一象限内抛物线上一点，过点 $P$ 作 $x$ 轴的垂线，交线段 $BC$ 于点 $F$，若四边形 $DEFP$ 为平行四边形，求点 $P$ 的坐标；标注答案点 $P$ 的坐标为 $\left(3,\dfrac{15}{8}\right)$解析由题意可得点 $B\left(4,0\right)$，点 $C\left(0,3\right)$．
可设抛物线的解析式为 $y=a\left(x+2\right)\left(x-4\right)$，
把点 $C\left(0,3\right)$ 的坐标代入，得 $a=-\dfrac{3}{8}$，
所以抛物线的解析式为 $y=-\dfrac{3}{8}\left(x+2\right)\left(x-4\right)=-\dfrac{3}{8}x^{2}+\dfrac{3}{4}x+3$．
所以顶点 $D$ 的坐标为 $\left(1,\dfrac{27}{8}\right)$．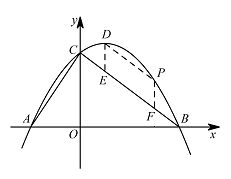
若四边形 $DEFP$ 是平行四边形，则有 $DP\parallel BC$．
可设直线 $DP$ 的解析式为 $y=-\dfrac{3}{4}x+n$，
把点 $D\left(1,\dfrac{27}{8}\right)$，得 $n=\dfrac{33}{8}$．
所以直线 $DP$ 的解析式为 $y=-\dfrac{3}{4}x+\dfrac{33}{8}$．
由题意可得 $\begin{cases}y=-\dfrac{3}{8}x^{2}+\dfrac{3}{4}+3,\\y-\dfrac{3}{4}x+\dfrac{33}{8}.\end{cases}$
解得 $x=3$ 或 $x=1$（舍去）．
所以把 $x=3$ 代入 $y=-\dfrac{3}{4}x+\dfrac{33}{8}$，得 $y=\dfrac{15}{8}$．
所以点 $P$ 的坐标为 $\left(3,\dfrac{15}{8}\right)$． -
设点 $M$ 是线段 $BC$ 上的一动点，过点 $M$ 作 $MN\parallel AB$，交 $AC$ 于点 $N$，点 $Q$ 从点 $B$ 出发，以每秒 $1$ 个单位长度的速度沿线段 $BA$ 向点 $A$ 运动，运动时间为 $t$（秒），当 $t$（秒）为何值时，存在 $\triangle QMN$ 为等腰直角三角形？标注答案当 $t=\dfrac{8}{3},\dfrac{14}{3}$ 或 $\dfrac{7}{2}$ 时，$\triangle QMN$ 为等腰直角三角形解析由题意可知 $0\leqslant t\leqslant 6$．
设直线 $AC$ 的解析式为 $y=m_{1}x+n_{1}$，
把 $A\left(-2,0\right)$ 和 $C\left(0,3\right)$ 代入 $y=m_{1}x+n_{1}$，
得 $\begin{cases}0=2m_{1}+n_{1},\\3=n_{1}.\end{cases}$ 解得 $\begin{cases}m_{1}=\dfrac{3}{2},\\n_{1}=3.\end{cases}$
所以直线 $AC$ 的解析式为 $y=\dfrac{3}{2}x+3$．
由题意知 $QB=t$．
① 如图，当 $\angle NMQ=90^{\circ}$ 时，$OQ=4-t$．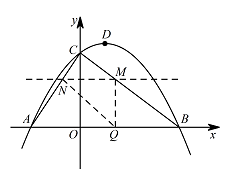
把 $x=4-t$ 代入 $y=-\dfrac{3}{4}x+3$ 中，得 $y=\dfrac{3}{4}t$．
所以点 $M\left(4-t,\dfrac{3}{4}t\right)$．
因为 $MN\parallel x轴$，所以 $N$ 的纵坐标为 $\dfrac{3}{4}t$．
把 $y=\dfrac{3}{4}t$ 代入 $y=\dfrac{3}{2}x+3$ 中，得 $x=\dfrac{1}{2}t-2$．
所以点 $N\left(\dfrac{1}{2}t-2, \dfrac{3}{4}t\right)$．
所以 $MN=\left(4-t\right)-\left(\dfrac{t}{2}-2\right)=6-\dfrac{3}{2}t$．
当 $MN=MQ$ 时，有 $6-\dfrac{3}{2}t=\dfrac{3}{4}t$．
所以 $t=\dfrac{8}{3}$，此时 $QB=\dfrac{8}{3}$，符合题意；
② 如图，当 $\angle QNM=90^{\circ}$ 时，点 $Q$ 的坐标为 $\left(4-t,0\right)$．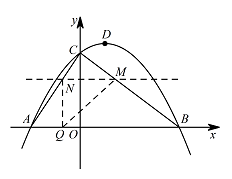
把 $x=4-t$ 代入 $y=\dfrac{3}{2}x+3$ 中，得 $y=9-\dfrac{3}{2}t$．
所以点 $N\left(4-t,9-\dfrac{3}{2}t\right)$．
因为 $MN\parallel x轴$，所以点 $M$ 的纵坐标为 $9-\dfrac{3}{2}t$．
把 $y=9-\dfrac{3}{2}t$ 代入 $y=-\dfrac{3}{4}x+3$ 中，得 $x=2t-8$．
所以点 $M\left(2t-8,9-\dfrac{3}{2}t\right)$．
所以 $MN=\left(2t-8\right)-\left(4-t\right)=3t-12$．
当 $NQ=MN$ 时，有 $9-\dfrac{3}{2}t=3t-12$，
所以 $t=\dfrac{14}{3}$，此时 $QB=\dfrac{14}{3}$，符合题意；
③ 如图，当 $\angle NQM=90^{\circ}$ 时．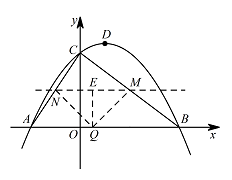
过点 $Q$ 作 $QE\perp MN$ 于点 $E$．
设 $QE=a$．把 $y=a$ 代入 $y=-\dfrac{3}{4}x+3$ 中，得 $x=4-\dfrac{4}{3}a$．
所以点 $M\left(4-\dfrac{4}{3}a,a\right)$．
把 $y=a$ 代入 $y=\dfrac{3}{2}x+3$ 中，得 $x=\dfrac{2}{3}a-2$．
所以点 $N\left(\dfrac{2}{3}a-2,a\right)$．
所以 $MN=\left(4-\dfrac{4}{3}a\right)-\left(\dfrac{2}{3}a-2\right)=6-2a$．
当 $MN=2QE$ 时，$\triangle QMN$ 为等腰直角三角形．
所以 $6-2a=2a$，即 $a=\dfrac{3}{2}$．
所以点 $M\left(2,\dfrac{3}{2}\right)$，点 $N\left(-1,\dfrac{3}{2}\right)$．
所以点 $E\left(\dfrac{1}{2},\dfrac{3}{2}\right)$．
所以点 $Q\left(\dfrac 12 ,0\right)$．
所以 $QB=4-\dfrac 12=\dfrac{7}{2}$．
所以 $t=\dfrac{7}{2}$，此情况符合题意．
综上所述，当 $t=\dfrac{8}{3}$ 或 $\dfrac{14}{3}$ 或 $\dfrac{7}{2}$ 时，$\triangle QMN$ 为等腰直角三角形．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
