已知函数 $f\left(x\right)$ 的图像在 $[a,b]$ 上连续不断,定义:\[\begin{split}&{f_1}\left(x\right) = \min \left\{ f\left(t\right)\left|\right.a \leqslant t \leqslant x\right\} \left(x \in \left[a,b\right]\right),\\&{f_2}\left(x\right) = \max \left\{ f\left(t\right)\left|\right.a \leqslant t \leqslant x\right\} \left(x \in \left[a,b\right]\right).\end{split}\]其中 $\min \left\{ f\left(x\right)\left|\right.x \in D\right)$ 表示函数 $f\left(x\right)$ 在 $D$ 上的最小值,$\max \left\{ f\left(x\right)\left|\right.x \in D\right)$ 表示函数 $f\left(x\right)$ 在 $D$ 上的最大值.若存在最小正整数 $k$,使得 ${f_2}\left(x\right) - {f_1}\left(x\right) \leqslant k\left(x - a\right)$ 对任意的 $x \in \left[a,b\right]$ 成立,则称函数 $f\left(x\right)$ 为 $\left[a,b\right]$ 上的" $k$ 阶收缩函数".
【难度】
【出处】
无
【标注】
-
若 $f\left(x\right) = \cos x,x \in \left[0,\pi \right]$,试写出 ${f_1}\left(x\right)$,${f_2}\left(x\right)$ 的表达式;标注答案${f_1}(x) = \cos x,x \in [0,\pi ]$,${f_2}(x) = 1,x \in [0,\pi ]$解析略
-
已知函数 $f\left(x\right) = {x^2},x \in \left[ - 1,4\right],$ 试判断 $f\left(x\right)$ 是否为 $[-1,4]$ 上的" $k$ 阶收缩函数",如果是,求出对应的 $k$,如果不是,请说明理由;标注答案是,$k=4$解析因为 ${f_1}(x) = {\begin{cases}{x^2},&x \in [ - 1,0) \\ 0,&x \in [0,4] \end{cases}}$,${f_2}(x) = {\begin{cases}1,&x \in [ - 1,1) \\{x^{^2}},&x \in [1,4] \end{cases}}$,所以\[{f_2}(x) - {f_1}(x) = {\begin{cases}1 - {x^2},&x \in [ - 1,0) \\1,&x\in [0,1) \\{x^2}, &x \in [1,4] \end{cases}}\]如图,$f(x)$ 是 $[-1,4]$ 上的" $4$ 阶收缩函数".
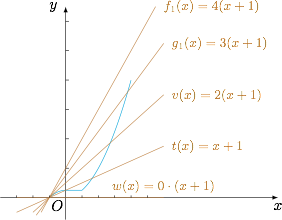
-
已知 $b > 0$,函数 $f\left(x\right) = - {x^3} + 3{x^2},$ 是 $[0,b]$ 上的 $2$ 阶收缩函数,求 $b$ 的取值范围.标注答案$\left(\dfrac {3-\sqrt 5}{2},1\right]$解析因为 $f_{1}(x)=\begin{cases}0,&0\leqslant x\leqslant 3\\ -x^{3}+3x^{2},&x>3\end{cases}$,$f_{2}(x)=\begin{cases}-x^{3}+3x^{2},&0\leqslant x\leqslant 2\\ 4,&x>2\end{cases}$,所以\[f_{2}(x)-f_{1}(x)=\begin{cases}-x^{3}+3x^{2},&0\leqslant x\leqslant 2\\ 4,&2<x\leqslant 3\\ 4+x^{3}-3x^{2},&x>3\end{cases}.\]如图,$\dfrac{3-\sqrt 5}{2}<b\leqslant 1$.
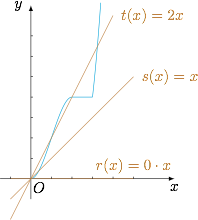
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3