如图，$ \odot E $ 的圆心 $ E\left(3,0\right) $，半径为 $ 5 $，$ \odot E $ 与 $ y $ 轴相交于 $ A,B $ 两点（点 $ A $ 在点 $ B $ 的上方），与 $ x $ 轴的正半轴相交于点 $ C $；直线 $ l $ 的解析式为 $ y= \dfrac{3}{4} x+4 $，与 $ x $ 轴相交于点 $ D $；以 $ C $ 为顶点的抛物线经过点 $ B $．
【难度】
【出处】
无
【标注】
-
求抛物线的解析式；标注答案$y=- \dfrac{1}{16} x^ 2+x-4 $解析连接 $ AE $．
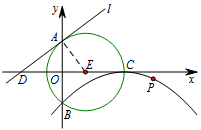由已知得 $ AE=CE=5 $，$ OE=3 $．
在 $ \mathrm {Rt}\triangle AOE $ 中，由勾股定理得 $ OA= \sqrt {A{E^2} - O{E^2}} = \sqrt {{5^2} - {3^2}} =4 $．
因为 $ OC\perp AB $，
所以由垂径定理得 $ OB=OA=4 $，$ OC=OE+CE=3+5=8 $，
所以 $ A\left(0,4\right) $，$ B\left(0,-4\right) $，$ C\left(8,0\right) $．
因为抛物线的顶点为点 $ C $，
所以设抛物线的解析式为 $ y=a\left(x-8\right)^2 $．
将点 $ B $ 的坐标代入上解析式，得 $ 64\cdot a=-4 $，故 $a=- \dfrac{1}{16}$．
所以 $ y=- \dfrac{1}{16} \left(x-8\right)^2 $，
所以 $y=- \dfrac{1}{16} x^ 2+x-4 $ 为所求抛物线的解析式． -
判断直线 $ l $ 与 $ \odot E $ 的位置关系，并说明理由；标注答案直线 $ l $ 与 $ \odot E $ 相切于点 $ A $解析在直线 $ l $ 的解析式 $ y= \dfrac{3}{4} x+4 $ 中，令 $ y=0 $，得 $ y= \dfrac{3}{4} x+4=0 $，解得 $x=-\dfrac{16}{3}$，
所以点 $ D $ 的坐标为 $ \left(- \dfrac{16}{3} ,0\right) $．
当 $ x=0 $ 时，$ y=4 $，所以点 $ A $ 在直线 $ l $ 上．
在 $ \mathrm {Rt}\triangle AOE $ 和 $ \mathrm {Rt}\triangle DOA $ 中，
因为 $ \dfrac{OE}{OA} = \dfrac{3}{4}$，$\dfrac{OA}{OD} = \dfrac{3}{4}$，
所以 $ \dfrac{OE}{OA} = \dfrac{OA}{OD}$．
因为 $ \angle AOE=\angle DOA=90^\circ $，
所以 $ \triangle AOE\backsim \triangle DOA $，
所以 $ \angle AEO=\angle DAO $．
因为 $\angle AEO+\angle EAO=90^\circ $，
所以 $ \angle DAO+\angle EAO=90^\circ $，即 $ \angle DAE=90^\circ $，
所以直线 $ l $ 与 $ \odot E $ 相切于点 $ A $． -
动点 $ P $ 在抛物线上，当点 $ P $ 到直线 $ l $ 的距离最小时，求出点 $ P $ 的坐标及最小距离．标注答案当抛物线上的动点 $ P $ 的坐标为 $ \left(2,- \dfrac{9}{4} \right) $ 时，点 $ P $ 到直线 $ l $ 的距离最小，其最小距离为 $\dfrac{31}{5}$解析
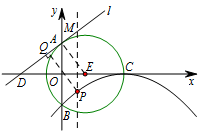过点 $ P $ 作直线 $ l $ 的垂线段 $ PQ $，垂足为 $ Q $，
过点 $ P $ 作直线 $ PM $ 垂直于 $ x $ 轴，交直线 $ l $ 于点 $ M $．
设 $ M\left(m, \dfrac{3}{4} m+4\right) $，$ P\left(m,- \dfrac{1}{16}m^ 2+m-4\right)$，
则 $PM= \dfrac{3}{4} m+4-\left(- \dfrac{1}{16} m^ 2+m-4\right)= \dfrac{1}{16} m^ 2- \dfrac{1}{4} m+8= \dfrac{1}{16}\left(m-2\right)^2+ \dfrac{31}{4}$．
当 $ m=2 $ 时，$ PM $ 取得最小值 $\dfrac{31}{4}$．
此时，$ P\left(2,- \dfrac{9}{4}\right)$．
因为 $PM\perp x $ 轴，
所以 $\angle QMP=\angle DAO=\angle AEO $．
因为 $\angle PQM=90^\circ $，
所以 $ \triangle PQM $ 的三个内角固定不变．
所以在动点 $ P $ 运动的过程中，$ \triangle PQM $ 的三边的比例关系不变．
所以当 $ PM $ 取得最小值时，$ PQ $ 也取得最小值．
$PQ_{最小}=PM_{最小}\cdot \sin \angle QMP=PM_{最小}\cdot \sin \angle AEO= \dfrac{31}{4} \times \dfrac{4}{5} = \dfrac{31}{5}$．
所以，当抛物线上的动点 $ P $ 的坐标为 $ \left(2,- \dfrac{9}{4} \right) $ 时，点 $ P $ 到直线 $ l $ 的距离最小，其最小距离为 $\dfrac{31}{5}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
