抛物线 $y=\dfrac 14x^2-\dfrac 32x+2$ 与 $x$ 轴交于 $A$,$B$ 两点($OA<OB$),与 $y$ 轴交于点 $C$.点 $P$ 从点 $O$ 出发,以每秒 $2$ 个单位长度的速度向点 $B$ 运动,同时点 $E$ 也从点 $O$ 出发,以每秒 $1$ 个单位长度的速度向点 $C$ 运动,设点 $P$ 的运动时间为 $t$ 秒($0<t<2$).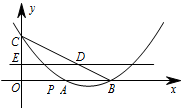

【难度】
【出处】
无
【标注】
-
过点 $E$ 作 $x$ 轴的平行线,与 $BC$ 相交于点 $D$(如图所示),当 $t$ 为何值时,$\dfrac{1}{OP}+\dfrac{1}{ED}$ 的值最小,求出这个最小值并写出此时点 $E,P$ 的坐标;标注答案$\dfrac{1}{OP}+\dfrac{1}{ED}$ 有最小值 $1$,此时点 $
E\left(0,1\right)$,点 $P\left(2,0\right)$解析在抛物线解析式中,令 $y=0$,即 $\dfrac 14x^2-\dfrac 32x+2=0$,
解得 $x_1=2$,$x_2=4$,
又 $OA<OB$,所以点 $A\left(2.0\right)$,点 $B\left(4,0\right)$.
在抛物线解析式中,令 $x=0$,得 $y=2$,
所以 $C\left(0,2\right)$.
由题意得 $OP=2t$,$OE=t$,
因为 $ DE\parallel OB$,
所以 $\triangle CDE\backsim \triangle
CBO$,
所以 $\dfrac{CE}{CO}=\dfrac{ED}{OB}$,即 $\dfrac{2-t}{2}=\dfrac{DE}{4}$,
所以 $DE=4-2t$,
所以 $\dfrac{1}{OP}+\dfrac{1}{ED}=\dfrac{1}{2t}+\dfrac{1}{4-2t}=\dfrac{1}{-t^2+2t}=\dfrac{1}{1-\left(t-1\right)^2}$.
因为 $ 0<t<2$,$1-\left(t-1\right)^2$ 始终为正数,且 $t=1$ 时,$1-\left(t-1\right)^2$ 有最大值 $1$,
所以 $t=1$ 时,$\dfrac{1}{1-\left(t-1\right)^2}$ 有最小值 $1$,
即 $t=1$ 时,$\dfrac{1}{OP}+\dfrac{1}{ED}$ 有最小值 $1$,此时 $OP=2$,$OE=1$.
所以点 $
E\left(0,1\right)$,点 $P\left(2,0\right)$. -
在满足第1问的条件下,抛物线的对称轴上是否存在点 $F$,使 $\triangle EFP$ 为直角三角形?若存在,请直接写出点 $F$ 的坐标;若不存在,请说明理由.标注答案存在,点 $F$ 的坐标为 $\left(3,2\right)$ 或 $\left(3,7\right)$解析因为抛物线 $y=\dfrac 14x^2+\dfrac 32x+2$ 的对称轴方程为 $x=3$.
设点 $F\left(3,m\right)$,所以 $EP^2=5$,$PF^2=\left(3-2\right)^2+m^2$,$EF^2=\left(m-1\right)^2+3^2$.
① 当 $\angle EPF=90^\circ$ 时,$PE^2+FP^2=EF^2$,
即 $5+\left(3-2\right)^2+m^2=\left(m-1\right)^2+3^2$,解得 $m=2$;
② 当 $\angle EFP=90^\circ$ 时,$EF^2+FP^2=PE^2$,
即 $\left(m-1\right)^2+3^2+\left(3-2\right)^2+m^2=5$,解得 $m=0$ 或 $m=1$,不合题意舍去.
所以当 $\angle EFP=90^\circ$ 时,这种情况不存在;
③ 当 $\angle PEF=90^\circ$ 时,$EF^2+PE^2=PF^2$,
即 $\left(m-1\right)^2+3^2+5=\left(3-2\right)^2+m^2$,解得 $m=7$.
综上所述,点 $F$ 的坐标为 $\left(3,2\right)$ 或 $\left(3,7\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2