如图，一次函数 $y=-2x+10$ 的图象与反比例函数 $y=\dfrac kx\left(k>0\right)$ 的图象相交于 $A,B$ 两点（点 $A$ 在点 $B$ 的右侧），分别交 $x,y$ 轴于点 $E,F$．
【难度】
【出处】
无
【标注】
-
若点 $A$ 的坐标为 $\left(4,2\right)$，反比例函数图象的另一支上是否存在一点 $P$，使 $\triangle PAB$ 是以 $AB$ 为直角边的直角三角形？若存在，求出所以符合条件的点 $P$ 的坐标：若不存在，请说明理由；标注答案存在，点 $P$ 坐标为 $\left(-4,-2\right)$ 或 $\left(-16,-\dfrac 12\right)$解析将点 $A\left(4,2\right)$ 坐标代入反比例函数解析式，得 $k=8$，
所以反比例函数解析式为 $y=\dfrac 8x$．
联立方程组 $\begin{cases}y=-2x+10,\\ y=\dfrac 8x,\end{cases}$
解得 $\begin{cases}x_1=4,\\y_1=2,\end{cases}\begin{cases}x_2=1,\\y_2=8.\end{cases}$
所以点 $B$ 的坐标为 $\left(1,8\right)$．
由题意可得点 $E\left(5,0\right),F\left(0,10\right)$．
以 $AB$ 为直角边的直角三角形有两种情况：
① 如图，当 $\angle P_1AB=90^\circ$ 时．
连接 $OA$，则 $OA=\sqrt{4^2+2^2}=2\sqrt 5$．
而 $AE=\sqrt{1^2+2^2}=\sqrt 5$，$OE=5$，
所以 $OA^2+AE^2=OE^2$，
所以 $A,O,P_1$ 三点共线．
由 $O,A$ 的坐标可求得直线 $AP_1$ 的解析式为 $y=\dfrac 12x$．
联立方程组 $\begin{cases}y=\dfrac 12x,\\ y=\dfrac 8x,\end{cases}$
解得 $\begin{cases}x_1=4,\\y_1=2,\end{cases}\begin{cases}x_2=-4,\\y_2=-2.\end{cases}$
所以点 $P_1$ 的坐标为 $\left(-4,-2\right)$；
② 如图，当 $\angle P_2BA=90^\circ$ 时，记 $BP_2$ 与 $y$ 轴的交点为 $G$．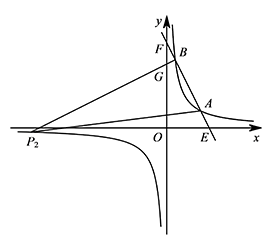
易证 $\triangle FBG\backsim \triangle FOE$，所以 $\dfrac{FB}{FG}=\dfrac{FO}{FE}$．
而 $FO=10$，$FE=\sqrt{5^2+10^2}=5\sqrt 5$，$FB=\sqrt{1^2+2^2}=\sqrt 5$，
可求得 $FG=\dfrac 52$，所以点 $G\left(0,\dfrac{15}2\right)$．
由 $B,G$ 的坐标可求得直线 $BP_2$ 的解析式为 $y=\dfrac 12x+\dfrac{15}{2}$．
联立方程组 $\begin{cases}y=\dfrac 12x+\dfrac{15}2,\\ y=\dfrac 8x,\end{cases}$
解得 $\begin{cases}x_1=1,\\y_1=8,\end{cases}\begin{cases}x_2=-16,\\y_2=-\dfrac 12.\end{cases}$
所以点 $P_2$ 的坐标为 $\left(-16,-\dfrac 12\right)$；
综上可得，满足条件的点 $P$ 坐标为 $\left(-4,-2\right)$ 或 $\left(-16,-\dfrac 12\right)$． -
当 $A\left(a,-2a+10\right),B\left(b,-2b+10\right)$ 时，直线 $OA$ 与此反比例函数图象的另一支交于另一点 $C$，连接 $BC$ 交 $y$ 轴于点 $D$，若 $\dfrac{BC}{BD}=\dfrac 52$，求 $\triangle ABC$ 的面积．标注答案$\triangle ABC$ 的面积为 $10$解析联立方程组 $\begin{cases}y=-2x+10,\\ y=\dfrac kx,\end{cases}$
整理得 $2x^2-10x+k=0$．
因为 $a,b$ 是关于 $x$ 的方程的两个实数根，
所以 $a+b=\dfrac{-10}{2}$，即 $a+b=5$．
又 $A,C$ 两点 关于原点 $O$ 对称，
所以点 $C$ 的坐标为 $\left(-a,2a-10\right)$．
过点 $B$ 作 $x$ 轴的垂线，过点 $C$ 作 $y$ 轴的垂线，两垂线交于点 $C_1$，过点 $D$ 作 $DD_1\perp BC_1$ 于点 $D_1$．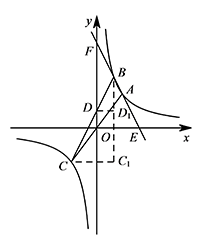
所以 $\dfrac{BC}{BD}=\dfrac{CC_1}{DD_1}=\dfrac 52$，即 $\dfrac{b+a}{b}=\dfrac 52$，
从而 $a=\dfrac 32b$．
解方程组 $\begin{cases}a+b=5,\\ a=\dfrac 32b,\end{cases}$ 得 $\begin{cases}a=3,\\b=2.\end{cases}$
所以点 $A\left(3,4\right)$，点 $B\left(2,6\right)$，点 $C\left(-3,-4\right)$，
所以 $S_{\triangle OAB}=S_{\triangle OEB}-S_{\triangle OAE}=\dfrac 12\times 5\times 6-\dfrac 12\times 5\times 4=5$．
所以 $S_{\triangle ABC}=2S_{\triangle OAB}=10$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
