如图，二次函数 $y=x^2+bx+c$ 的图象交 $x$ 轴于 $A\left(-1,0\right),B\left(3,0\right)$ 两点，交 $y$ 轴于点 $C$，连接 $BC$，动点 $P$ 以每秒 $1$ 个单位长度的速度从 $A$ 向 $B$ 运动，动点 $Q$ 以每秒 $\sqrt2$ 个单位长度的速度从 $B$ 向 $C$ 运动，$P,Q$ 同时出发，连接 $PQ$，当点 $Q$ 到达 $C$ 点时，$P,Q$ 同时停止运动，设运动时间为 $t$ 秒．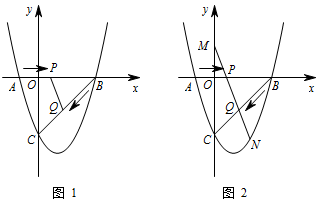
【难度】
【出处】
无
【标注】
-
如图 1，当 $\triangle BPQ$ 为直角三角形时，求 $t$ 的值；标注答案$t=\dfrac43$ 或 $2$解析因为二次函数 $y=x^2+bx+c$ 的图象经过 $A\left(-1,0\right),B\left(3,0\right)$ 两点，
所以 $\begin{cases}1-b+c=0,\\9+3b+c=0,\end{cases}$ 解得 $\begin{cases}b=-2,\\c=-3.\end{cases}$
所以二次函数的解析式是 $y=x^2-2x-3$．
因为 $y=x^2-2x-3$，
所以点 $C$ 的坐标是 $\left(0,-3\right)$，
所以 $BC=\sqrt{\left(3-0\right)^2+\left[0-\left(-3\right)\right]^2}=3\sqrt2$．
设 $BC$ 所在的直线的解析式是 $y=mx+n$，
则 $\begin{cases}3m+n=0,\\n=-3,\end{cases}$ 解得 $\begin{cases}m=1,\\n=-3.\end{cases}$
所以 $BC$ 所在的直线的解析式是 $y=x-3$．
因为经过 $t$ 秒，$AP=t$，$BQ=\sqrt2t$，
所以点 $P$ 的坐标是 $\left(t-1,0\right)$．
设点 $Q$ 的坐标是 $\left(x,y\right)$，
因为 $OB=OC=3$，所以 $\angle OBC=\angle OCB=45^\circ$，
则 $y=-\sqrt2\times\sin {45^\circ}=-\sqrt2t\times \dfrac{\sqrt2}{2}=-t$，
所以点 $Q$ 的坐标是 $\left(3-t,-t\right)$．
① 当 $\angle QPB=90^\circ$ 时，如图．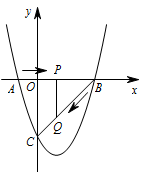
此时点 $P$ 和点 $Q$ 的横坐标相同
所以 $t-1=3-t$，解得 $t=2$．
即当 $t=2$ 时，$\triangle BPQ$ 为直角三角形．
② 当 $\angle PQB=90^\circ$ 时，如图．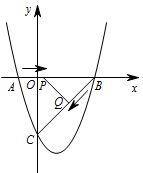
因为 $\angle PBQ=45^\circ$，所以 $BP=\sqrt 2BQ$，
因为 $BQ=\sqrt2t$，所以 $BP=2t$，
所以 $OP=3-2t$，
所以 $3-2t=t-1$，解得 $t= \dfrac43$．
即当 $t=\dfrac43$ 时，$\triangle BPQ$ 为直角三角形．
综上可得，当 $\triangle BPQ$ 为直角三角形，$t=\dfrac43$ 或 $2$． -
如图 2，当 $t<2$ 时，延长 $QP$ 交 $y$ 轴于点 $M$，在抛物线上是否存在一点 $N$，使得 $PQ$ 的中点恰为 $MN$ 的中点？若存在，求出点 $N$ 的坐标与 $t$ 的值；若不存在，请说明理由．标注答案存在，点 $N$ 的坐标为 $\left(2,-3\right)$，$t=\dfrac{9-\sqrt{33}}{2}$解析如图，延长 $MQ$ 交抛物线于点 $N$，$H$ 是 $PQ$ 的中点，
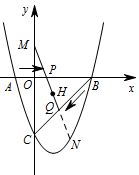设 $PQ$ 所在的直线的解析式是 $y=cx+d$，
因为点 $P$ 的坐标是 $\left(t-1,0\right)$，点 $Q$ 的坐标是 $\left(3-t,-t\right)$，
所以 $\begin{cases}c\left(t-1\right)+d=0,\\c\left(3-t\right)+d=-t,\end{cases}$ 解得 $\begin{cases}c=\dfrac{t}{2t-4},\\d=\dfrac{t-t^2}{2t-4.}\end{cases}$
所以 $PQ$ 所在的直线的解析式是 $y=\dfrac{t}{2t-4} x+\dfrac{t-t^2}{2t-4}$，
所以点 $M$ 的坐标是 $\left(0,\dfrac{t-t^2}{2t-4} \right)$，
因为 $\dfrac{t-1+3-t}{2}=1$，$\dfrac{-t+0}{2}=-\dfrac t2$，
所以 $PQ$ 的中点 $H$ 的坐标是 $\left(1,-\dfrac t2 \right)$．
假设 $PQ$ 的中点恰为 $MN$ 的中点，
可得点 $N$ 的坐标是 $\left(2, \dfrac{3t-t^2}{2t-4}\right)$，
因为点 $N$ 在抛物线上，则 $\dfrac{3t-t^2}{2t-4}=2^2-2\times 2-3=-3$，
解得 $t=\dfrac{\sqrt{33}+9}{2} $ 或 $t=\dfrac{9-\sqrt{33}}{2}$，
而 $t<2$，所以 $t=\dfrac{9-\sqrt{33}}{2}$，
此时点 $N\left(2,-3\right)$．
所以当 $t=\dfrac{9-\sqrt{33}}{2}$ 时，延长 $QP$ 交 $y$ 轴于点 $M$，在抛物线上存在一点 $N\left(2,-3\right)$，使得 $PQ$ 的中点恰为 $MN$ 的中点．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
