如图，$C$ 为 $\angle AOB$ 的边 $OA$ 上一点，$OC=6$，$ N $ 为边 $OB$ 上异于点 $O$ 的一动点，$P$ 是线段 $CN$ 上一点，过点 $P$ 分别作 $PQ\parallel OA$ 交 $OB$ 于点 $Q$，$PM\parallel OB$ 交 $OA$ 于点 $M$．当点 $N$ 在边 $OB$ 上运动时，四边形 $OMPQ$ 始终保持为菱形．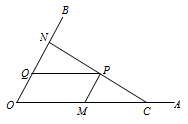
【难度】
【出处】
无
【标注】
-
问：$\dfrac {1}{OM}-\dfrac {1}{ON}$ 的值是否发生变化？如果变化，求出其取值范围；如果不变，请说明理由．标注答案不发生变化，$\dfrac {1}{OM}-\dfrac {1}{ON}=\dfrac 16$解析设 $OM=x$，$ON=y$．
因为四边形 $OMPQ$ 为菱形，
所以 $ OQ=QP=OM=x$，$NQ=y-x$．
因为 $PQ\parallel OA$，
所以 $\angle NQP=\angle O$．
又 $\angle QNP=\angle ONC$，
所以 $ \triangle NQP\backsim \triangle NOC$，
所以 $ \dfrac {QP}{OC}=\dfrac {NQ}{ON}$，即 $\dfrac x6=\dfrac {y-x}{y}$，
所以 $ 6y-6x=xy$，两边都除以 $6xy$，得 $\dfrac 1x-\dfrac 1y=\dfrac 16$，
即 $\dfrac {1}{OM}-\dfrac {1}{ON}=\dfrac 16$． -
设菱形 $OMPQ$ 的面积为 $S_{1}$，$\triangle NOC$ 的面积为 $S_{2}$，求 $\dfrac {S_1}{S_2}$ 的取值范围．标注答案$0< \dfrac {S_1}{S_2}\leqslant \dfrac 12$解析如图，过 $P$ 作 $PE\perp OA$ 于 $E$，过 $N$ 作 $NF\perp OA$ 于 $F$．
则 $S_{1}=OM\cdot PE$，$S_{2}=OC\cdot NF$，
所以 $\dfrac {S_1}{S_2}=\dfrac {x\cdot PE}{3NF}$．
因为 $PM\parallel OB$，
所以 $ \angle CMP=\angle O$．
又 $\angle PCM=\angle NCO$，
所以 $\triangle CPM\backsim \triangle CNO$，
所以 $\dfrac {PE}{NF}=\dfrac {CM}{CO}=\dfrac {6-x}{6}$，
所以 $\dfrac {S_1}{S_2}=\dfrac {x\left(6-x\right)}{18}=-\dfrac {1}{18}\left(x-3\right)^2+\dfrac 12$．
因为 $ 0<x<6$，由这个二次函数的图象可知，$0< \dfrac {S_1}{S_2}\leqslant \dfrac 12$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
