如图1，抛物线 $y=-\dfrac 35[(x-2)^2+n]$ 与 $x$ 轴交于 $A(m-2,0),B(2m+3,0)$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C$，连接 $BC$．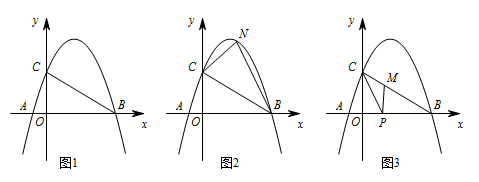
【难度】
【出处】
无
【标注】
-
如图2，点 $N$ 为抛物线上的一动点，且位于直线 $BC$ 上方，连接 $CN,BN$．求 $\triangle NBC$ 面积的最大值；标注答案$\triangle NBC$ 面积的最大值为 $\dfrac{75}{8}$解析因为抛物线的解析式为 $y=-\dfrac 35[(x-2)^2+n]=-\dfrac 35(x-2)^2-\dfrac35n$，
所以抛物线的对称轴为直线 $x=2$，
因为点 $A$ 和点 $B$ 为对称点，
所以 $2-(m-2)=2m+3-2$，解得 $m=1$，
所以点 $A,B$ 的坐标分别为 $(-1,0),(5,0)$．
把点 $A(-1,0)$ 的坐标代入抛物线解析式得 $9+n=0$，即 $n=-9$．
所以抛物线解析式为 $y=-\dfrac 35 [(x-2)^2-9]=-\dfrac 35 x^2+\dfrac{12}{5} x+3$，
所以点 $C$ 的坐标为 $(0,3)$．
从而直线 $BC$ 的解析式为 $y=-\dfrac 35 x+3$．
作 $ND\parallel y$ 轴交 $BC$ 于点 $D$．
设点 $N$ 的坐标为 $\left(x,-\dfrac35 x^2+ \dfrac{12}{5}x+3\right)$，则点 $D$ 的坐标为 $\left(x,-\dfrac 35x+3\right)$．
所以 $ND=-\dfrac 35 x^2+\dfrac{12}{5} x+3-\left(-\dfrac 35 x+3\right)=-\dfrac 35 x^2+3x$，
所以 $S_{\triangle NBC}=S_{\triangle NDC}+S_{\triangle NDB}= \dfrac 12\times5\times ND=-\dfrac 32x^2+\dfrac{15}{2}x=-\left(x-\dfrac 52\right)^2+\dfrac{75}{8}$，
当 $x=\dfrac 52$ 时，$\triangle NBC$ 面积最大，最大值为 $\dfrac{75}{8}$． -
如图3，点 $M,P$ 分别为线段 $BC$ 和线段 $OB$ 上的动点，连接 $PM,PC$，是否存在这样的点 $P$，使 $\triangle PCM$ 为等腰三角形，$\triangle PMB$ 为直角三角形同时成立？若存在，求出点 $P$ 的坐标；若不存在，请说明理由．标注答案存在．点 $P$ 的坐标为 $\left(\dfrac 34 ,0\right)$ 或 $\left(\dfrac{3\sqrt{34}-9}{5},0\right)$解析因为点 $B(5,0)$，点 $C(0,3)$，
所以 $BC=\sqrt{3^2+5^2} =\sqrt{34}$．
① 当 $\angle PMB=90^\circ$，则 $\angle PMC=90^\circ$，
所以 $\triangle PMC$ 为等腰直角三角形，$MP=MC$．
设 $PM=t$，则 $CM=t$，$MB=\sqrt{34}-t$，
因为 $\angle MBP=\angle OBC$，所以 $\triangle BMP\backsim \triangle BOC$，
所以 $\dfrac{PM}{OC}=\dfrac{BM}{OB} =\dfrac{BP}{BC}$，即 $\dfrac t3 =\dfrac{\sqrt {34}-t}{5} =\dfrac{BP}{\sqrt{34}}$，
解得 $t=\dfrac{3\sqrt{34}}{8}$，$BP=\dfrac{17}{4}$，
所以 $OP=OB-BP=5-\dfrac{17}{4} =\dfrac 34$．
此时 $P$ 点坐标为 $\left(\dfrac 34 ,0\right)$；
② 当 $ \angle MPB=90^\circ $，则 $MP=MC$．
设 $PM=t$，则 $CM=t$，$MB=\sqrt{34}-t$，
因为 $\angle MBP=\angle CBO$，
所以 $\triangle BMP\backsim \triangle BCO$，
所以 $\dfrac{PM}{OC}=\dfrac{BM}{BC}=\dfrac{BP}{BO}$，即 $\dfrac t3 =\dfrac{\sqrt {34}-t}{\sqrt{34}}=\dfrac{BP}{5}$，
解得 $t=\dfrac{102-9\sqrt{34}}{25}$，$BP=\dfrac{34-3\sqrt{34}}{5}$，
所以 $OP=OB-BP=5-\dfrac{34-3\sqrt{34}}{5}=\dfrac{3\sqrt{34}-9}{5}$．
此时 $P$ 点坐标为 $ \left(\dfrac{3\sqrt{34}-9}{5},0\right)$．
综上所述，点 $P$ 的坐标为 $\left(\dfrac 34,0\right)$ 或 $\left(\dfrac{3\sqrt{34}-9}{5},0\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
