在平面直角坐标系中，抛物线 $y=-\dfrac 12x^2+bx+c$ 与 $x$ 轴交于点 $A,B$，与 $y$ 轴交于点 $C$，直线 $y=x+4$ 经过 $A,C$ 两点，点 $P$ 为 $AC$ 上方的抛物线上的动点．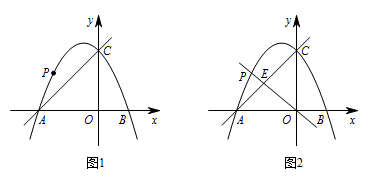
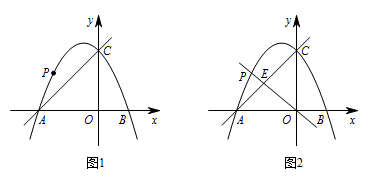
【难度】
【出处】
无
【标注】
-
如图1，当点 $P$ 运动到某位置时，以 $AP,AO$ 为邻边的平行四边形第四个顶点恰好也在抛物线上，求出此时点 $P$ 的坐标；标注答案$ P$ 点的坐标是 $\left(-3,\dfrac 52\right)$解析因为直线 $y=x+4$ 经过 $A,C$ 两点，
所以 $ A$ 点坐标是 $\left(-4,0\right)$，$C$ 点的坐标是 $ \left(0,4\right) $．
又抛物线过 $A,C$ 两点，
所以 $\begin{cases}-\dfrac 12\times\left(-4\right)^2-4b+c=0,\\ c=4,\end{cases}$ 解得 $\begin{cases}b=-1,\\ c=4.\end{cases}$
所以抛物线的解析式为 $y=-\dfrac 12x^2-x+4$，对称轴为 $x=-1$．
如图，以 $AP,AO$ 为邻边的平行四边形的第四个顶点 $Q$ 恰好也在抛物线上，
则 $PQ\parallel AO$，$PQ=AO=4$．
因为 $ P,Q$ 都在抛物线上，
所以 $P,Q$ 关于直线 $x=-1$ 对称，
所以 $ P$ 点的横坐标是 $-3$，$Q$ 点的横坐标为 $1$．
当 $x=-3$ 时，$y=-\dfrac 12\times \left(-3\right)^2-\left(-3\right)+4=\dfrac 52$，
所以 $ P$ 点的坐标是 $\left(-3,\dfrac 52\right)$． -
如图2，过点 $O,P$ 的直线 $y=kx$ 交 $AC$ 于点 $E$，若 $PE:OE=3:8$，求 $k$ 的值．标注答案$k=-\dfrac 92$ 或 $k=-\dfrac 56$解析如图，过 $P$ 点作 $PF\parallel OC$ 交 $AC$ 于点 $F$．
因为 $PF\parallel OC$，
所以 $\triangle PEF\backsim\triangle OEC$，
所以 $\dfrac{PE}{OE}=\dfrac{PF}{OC}$．
又 $ \dfrac{PE}{OE}=\dfrac 38 $，$ OC=4 $，
所以 $ PF=\dfrac 32$．
设点 $P$ 的坐标为 $\left(m,-\dfrac 12m^2-m+4\right)$，则点 $F$ 的坐标为 $\left(m,m+4\right) $，
所以 $PF=\left(-\dfrac 12m^2-m+4\right)-\left(m+4\right)=\dfrac 32$，
化简得 $m^2+4m+3=0$，
解得 $m_1=-1$，$m_2=-3$．
所以点 $P$ 的坐标为 $\left(-1,\dfrac 92\right)$ 或 $\left(-3,\dfrac 52\right)$．
又点 $P$ 在直线 $y=kx$ 上，
所以 $k=-\dfrac 92$ 或 $k=-\dfrac 56$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
