如图,抛物线 $y=-x^2+bx+c$ 交 $x$ 轴于点 $A\left(-3,0\right)$ 和点 $B$,交 $y$ 轴于点 $C\left(0,3\right)$.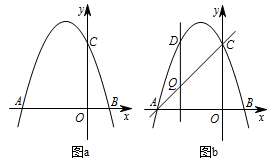

【难度】
【出处】
无
【标注】
-
若点 $P$ 在抛物线上,且 $S_{\triangle AOP}=4S_{\triangle BOC}$,求点 $P$ 的坐标;标注答案点 $P$ 的坐标为 $\left(-1,4\right)$ 或 $\left(-1+2\sqrt 2,-4\right)$ 或 $\left(-1-2\sqrt 2,-4\right)$解析把 $A\left(-3,0\right)$,$C\left(0,3\right)$ 代入 $y=-x^2+bx+c$,
得 $\begin{cases} 0=-9-3b+c, \\ 3=c,\end{cases}$ 解得 $\begin{cases} b=-2, \\ c=3.\end{cases}$
故该抛物线的解析式为 $y=-x^2-2x+3$.
则易得 $B\left(1,0\right)$.
因为 $S_{\triangle AOP}=4S_{\triangle BOC}$,
所以 $\dfrac 12\times 3\times \left |-x^2-2x+3 \right|=4\times \dfrac 12\times 1\times 3$.
整理得 $\left(x+1\right)^2=0$ 或 $x^2+2x-7=0$,
解得 $x=-1$ 或 $x=-1\pm2 \sqrt 2$.
则符合条件的点 $P$ 的坐标为 $\left(-1,4\right)$ 或 $\left(-1+2\sqrt 2,-4\right)$ 或 $\left(-1-2\sqrt 2,-4\right)$. -
如图 b,设点 $Q$ 是线段 $AC$ 上的一动点,作 $DQ\perp x$ 轴,交抛物线于点 $D$,求线段 $DQ$ 长度的最大值.标注答案$QD$ 有最大值 $\dfrac 94$解析设直线 $AC$ 的解析式为 $y=kx+t$,将 $A\left(-3,0\right)$,$C\left(0,3\right)$ 代入,
得 $\begin{cases} -3k+t=0, \\ t=3,\end{cases}$ 解得 $\begin{cases} k=1, \\ t=3.\end{cases}$
即直线 $AC$ 的解析式为 $y=x+3$.
设 $Q$ 点坐标为 $\left(x,x+3\right)\left(-3\leqslant x\leqslant 0\right)$,则 $D$ 点坐标为 $\left(x,-x^2-2x+3\right)$,
$QD=\left(-x^2-2x+3\right)-\left(x+3\right)=-x^2-3x=-\left(x+\dfrac 32\right)^2+\dfrac 94$,
所以当 $x=-\dfrac 32$ 时,$QD$ 有最大值 $\dfrac 94$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2