如图,抛物线 $ y=x^{2}+\dfrac{9}{2}x-3 $ 与直线 $y=\dfrac{1}{ 2}x-3$ 交于 $A,B$ 两点,其中点 $A$ 在 $y$ 轴上,点 $B$ 坐标为 $\left(-4,-5\right)$,点 $P$ 为 $y$ 轴左侧的抛物线上一动点,过点 $P$ 作 $PC\perp x$ 轴于点 $C$,交 $AB$ 于点 $D$.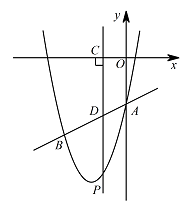

【难度】
【出处】
无
【标注】
-
以 $O,A,P,D$ 为顶点的平行四边形是否存在?如存在,求点 $P$ 的坐标;若不存在,请说明理由.标注答案存在,点 $P$ 的坐标为 $\left(-1,-\dfrac{13}{2}\right),\left(-3,-\dfrac{15}{2}\right)$ 或 $\left(-2-\sqrt{7},-1-\dfrac{\sqrt{7}}{2}\right)$解析设点 $P$ 的坐标为 $\left(a,a^{2}+\dfrac{9}{2}a-3\right)\left(a<0\right)$,则点 $D$ 的坐标为 $\left(a,\dfrac{1}{2}a-3\right)$,
所以 $PD=\left|a^{2}+4a\right|$.
若以 $O,A,P,D$ 为顶点的四边形是平行四边形,而 $PD\parallel AO$,
所以 $PD=OA=3$,即 $\left|a^{2}+4a\right|=3$.
① 当 $a^{2}+4a=3$ 时,解得 $a_{1}=-2-\sqrt{7}$,$a_{2}=-2+\sqrt{7}$(舍去)
② 当 $a^{2}+4a=-3$ 时,解得 $a_{1}=-1$,$a_{2}=-3$.
所以点 $P$ 的坐标为 $\left(-1,-\dfrac{13}{2}\right),\left(-3,-\dfrac{15}{2}\right)$ 或 $\left(-2-\sqrt{7},-1-\dfrac{\sqrt{7}}{2}\right)$. -
当点 $P$ 运动到直线 $AB$ 下方某一处时,过点 $P$ 作 $PM\perp AB$,垂足为 $M$,连接 $PA$ 使 $\triangle PAM$ 为等腰直角三角形,请直接写出此时点 $P$ 的坐标.标注答案点 $P$ 的坐标为 $\left(-\dfrac{3}{2},-\dfrac{15}{2}\right)$解析如图,过 $M$ 作 $y$ 轴的平行线 $EF$,过点 $A,P$ 作 $x$ 轴的平行线,分别交 $EF$ 于点 $E,F$.
 若 $\triangle PAM$ 为等腰直角三角形,则 $MA=MP$,
若 $\triangle PAM$ 为等腰直角三角形,则 $MA=MP$,
所以 $\triangle AEM\cong \triangle MFP$,
所以 $AE=MF$,$ME=PF$.
设点 $M$ 的坐标为 $\left(m,\dfrac 12m-3\right)$,点 $P$ 的坐标为 $\left(n,n^{2}+\dfrac{9}{2}n-3\right)\left(-4<n<0\right)$,
则 $AE=-m$,$ME=-3-\left(\dfrac 12m-3\right)=-\dfrac 12m$,
$MF=\dfrac 12m-3-\left(n^{2}+\dfrac{9}{2}n-3\right)=\dfrac 12m-n^2-\dfrac 92n$,$PF=n-m$.
从而 $\begin{cases}\dfrac 12m-n^2-\dfrac 92n=-m,\\-\dfrac 12m=n-m,\end{cases}$ 解得 $\begin{cases}m=-3,\\n=-\dfrac 32.\end{cases}$
所以点 $P$ 的坐标为 $\left(-\dfrac{3}{2},-\dfrac{15}{2}\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2