如图，平面直角坐标系 $xOy$ 中，抛物线 $y=x^2-4x+3 $ 与 $ x$ 轴交于点 $ A,B$，与 $y $ 轴交于点 $C$．若抛物线的对称轴上的点 $P$ 满足 $ \angle APB=\angle ACB$，求点 $P$ 的坐标．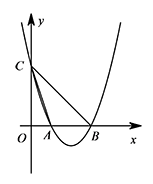
【难度】
【出处】
无
【标注】
【答案】
$P_1\left(2,2+\sqrt 5\right) $，$P_2\left(2,-2-\sqrt 5\right) $
【解析】
由已知可得 $A\left(1,0\right)$，$B\left(3,0\right)$，$C\left(0,3\right)$．
可设 $\triangle ABC$ 外接圆圆心为 $D(2,m)$，
则 $DC=DA$，即 $1+m^2=4+(m-3)^2$，
解得 $m=2$，
所以外接圆的圆心为 $\left(2,2\right)$，$DA=\sqrt 5$，
如图，该圆交抛物线对称轴于点 $ P_1$，作 $ P_1$ 关于 $x$ 轴的对称点 $ P_2$，则 $P_1,P_2$ 即为所求．
所以 $P_1\left(2,2+\sqrt 5\right) $，$P_2\left(2,-2-\sqrt 5\right) $．
可设 $\triangle ABC$ 外接圆圆心为 $D(2,m)$，
则 $DC=DA$，即 $1+m^2=4+(m-3)^2$，
解得 $m=2$，
所以外接圆的圆心为 $\left(2,2\right)$，$DA=\sqrt 5$，
如图，该圆交抛物线对称轴于点 $ P_1$，作 $ P_1$ 关于 $x$ 轴的对称点 $ P_2$，则 $P_1,P_2$ 即为所求．所以 $P_1\left(2,2+\sqrt 5\right) $，$P_2\left(2,-2-\sqrt 5\right) $．
答案
解析
备注
