如图1，直线 $y=-\dfrac 43x+4$ 交 $x$ 轴于点 $A$，交 $y$ 轴于点 $C\left(0,4\right)$，抛物线 $y=\dfrac 23x^2-\dfrac 43x-2$ 经过点 $A$，交 $y$ 轴于点 $B\left(0,-2\right)$．点 $P$ 为抛物线上的一个动点，过点 $P$ 作 $x$ 轴的垂线 $PD$，过点 $B$ 作 $BD\perp PD$ 于点 $D$，连接 $PB$．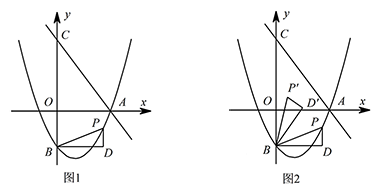
【难度】
【出处】
无
【标注】
-
当 $\triangle BDP$ 为等腰直角三角形时，求线段 $PD$ 的长．标注答案$PD$ 的长为 $\dfrac 72$ 或 $\dfrac 12$解析由点 $P$ 的横坐标为 $m$，得点 $P\left(m,\dfrac 23m^2-\dfrac 43m-2\right)$，点 $D\left(m,-2\right)$．
若 $\triangle BDP$ 为等腰直角三角形时，则 $PD=BD$．
① 当点 $P$ 在直线 $BD$ 上方时，$PD=\dfrac 23m^2-\dfrac 43m-2+2=\dfrac 23m^2-\dfrac 43m$，
ⅰ）若 $P$ 在 $y$ 轴左侧，则 $m<0$，$BD=-m$．
所以 $\dfrac 23m^2-\dfrac 43m=-m$，解得 $m=\dfrac 12$ 或 $m=0$（舍去）；
ⅱ）若 $P$ 在 $y$ 轴右侧，则 $m>0$，$BD=m$．
所以 $\dfrac 23m^2-\dfrac 43m=m$，解得 $m=\dfrac 72$ 或 $m=0$（舍去）；
② 当点 $P$ 在直线 $BD$ 下方时，$PD=-2-\left(\dfrac 23m^2-\dfrac 43m-2\right)=-\dfrac 23m^2+\dfrac 43m$，
则 $m>0$，$BD=m$．
所以 $-\dfrac 23m^2+\dfrac 43m=m$，解得 $m=\dfrac 12$ 或 $m=0$（舍去）．
综上可得，$m=\dfrac 72$ 或 $m=\dfrac 12$．
即当 $\triangle BDP$ 为等腰直角三角形时，$PD$ 的长为 $\dfrac 72$ 或 $\dfrac 12$． -
如图2，将 $\triangle BDP$ 绕点 $B$ 逆时针旋转，得到 $\triangle BD'P'$，且 $\angle PBP'=\angle OAC$，当点 $P$ 的对应点 $P'$ 落在坐标轴上时，请直接写出 $P$ 点的坐标．标注答案点 $P$ 的坐标为 $\left(-\sqrt 5,\dfrac{4\sqrt 5+4}{3}\right),\left(\sqrt 5,\dfrac{-4\sqrt 5+4}{3}\right)$ 或 $\left(\dfrac{25}{8},\dfrac{11}{32}\right)$解析由 $OA=3$，$OC=4$，可得 $AC=5$．
因为 $\angle PBP'=\angle OAC$，$\angle DBD'=\angle PBP'$，
所以 $\sin\angle DBD'=\dfrac 45$，$\cos\angle DBD'=\dfrac 35$，$\tan\angle DBD'=\dfrac 43$．
设点 $P$ 的坐标为 $\left(m,\dfrac 23m^2-\dfrac 43m-2\right)$．
① 当点 $P'$ 落在 $x$ 轴上时．
过点 $D'$ 作 $D'N\perp x$ 轴于点 $N$，交 $BD$ 于点 $M$，则 $\angle DBD'=\angle ND'P'$．
i）如图1，当点 $P'$ 在 $x$ 轴负半轴上时，则 $BD=-m$，$PD=\dfrac 23m^2-\dfrac 43m$．
由 $D'N-D'M=BO=2$，可得 $\dfrac 35\times\left(\dfrac 23m^2-\dfrac 43m\right)-\left(-\dfrac 45m\right)=2$，
解得 $m_1=-\sqrt 5$，$m_2=\sqrt 5$（舍去）；
ii）如图2，当点 $P'$ 在 $x$ 轴正半轴上时，则 $BD=m$，$PD=\dfrac 23m^2-\dfrac 43m$．
由 $D'M+D'N=2$，可得 $\dfrac 45m+\dfrac 35\times\left(\dfrac 23m^2-\dfrac 43m\right)=2$．
解得 $m_1=-\sqrt 5$（舍去），$m_2=\sqrt 5$．
此时点 $P$ 的坐标为 $\left(-\sqrt 5,\dfrac{4\sqrt 5+4}{3}\right)$ 或 $\left(\sqrt 5,\dfrac{-4\sqrt 5+4}{3}\right)$．
② 当点 $P'$ 落在 $y$ 轴上时．
如图3，过点 $D'$ 作 $D'M\perp x$ 轴交 $BD$ 于点 $M$，过点 $P'$ 作 $P'N\perp y$ 轴，交 $MD'$ 的延长线于点 $N$，则 $\angle DBD'=\angle ND'P'$．
显然 $PN=BM$，
所以 $\dfrac 45\times\left(\dfrac 23m^2-\dfrac 43m\right)=\dfrac 35m$，解得 $m_1=0$（舍去），$m_2=\dfrac{25}8$．
此时点 $P$ 的坐标为 $\left(\dfrac{25}{8},\dfrac{11}{32}\right)$．
综上所述，此时点 $P$ 的坐标为 $\left(-\sqrt 5,\dfrac{4\sqrt 5+4}{3}\right),\left(\sqrt 5,\dfrac{-4\sqrt 5+4}{3}\right)$ 或 $\left(\dfrac{25}{8},\dfrac{11}{32}\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
