如图，抛物线 $y=-x^2+4x$ 过 $A\left(4,0\right),B\left(1,3\right)$ 两点，点 $C,B$ 关于抛物线的对称轴对称，过点 $B$ 作直线 $BH\perp x$ 轴，交 $x$ 轴于点 $H$．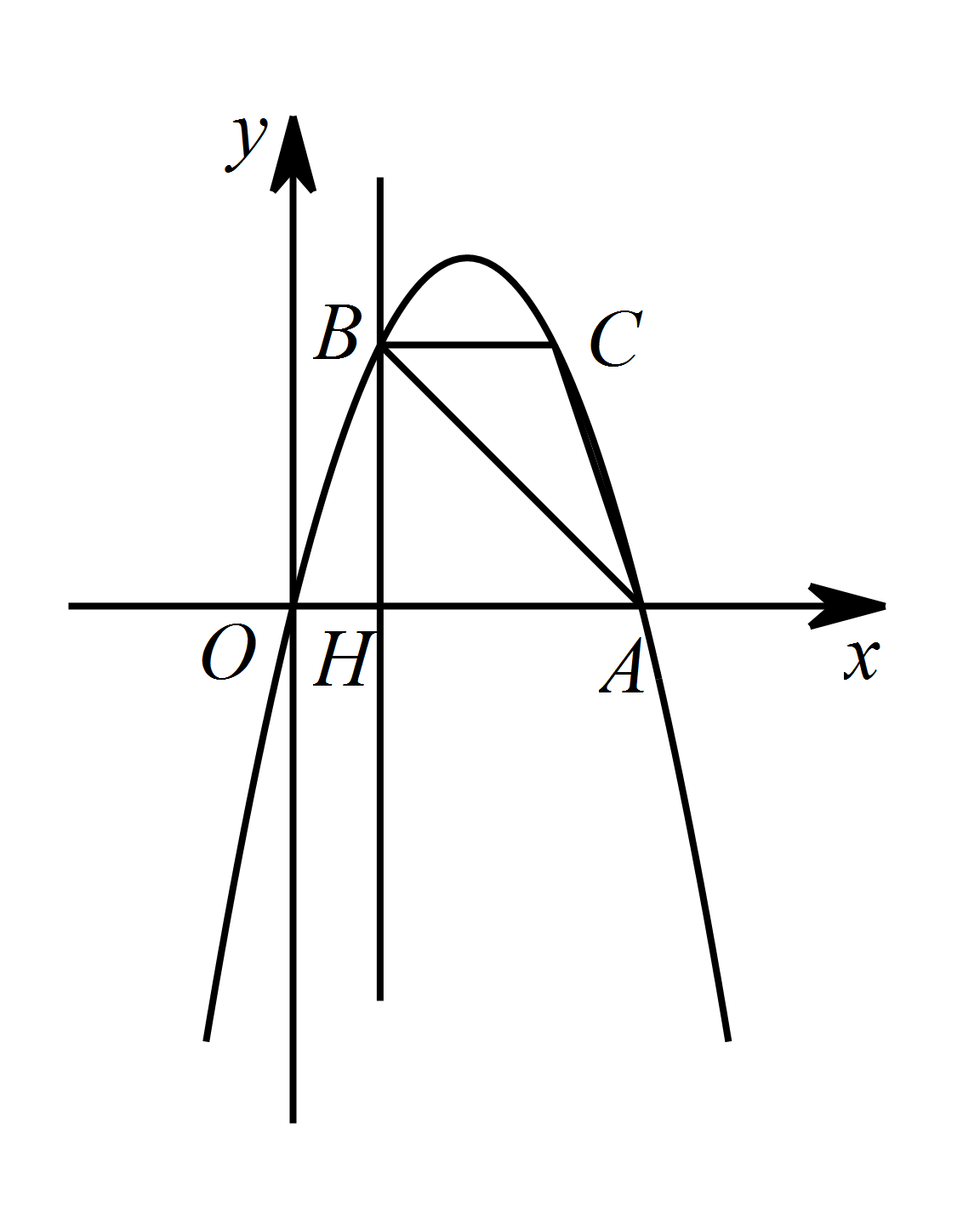
【难度】
【出处】
无
【标注】
-
点 $P$ 是抛物线上一动点，且位于第四象限，当 $\triangle ABP$ 的面积为 $6$ 时，求出点 $P$ 的坐标；标注答案点 $P$ 坐标为 $\left(5,-5\right)$解析过点 $P$ 作 $PD\perp BH$ 交 $BH$ 于点 $D$，
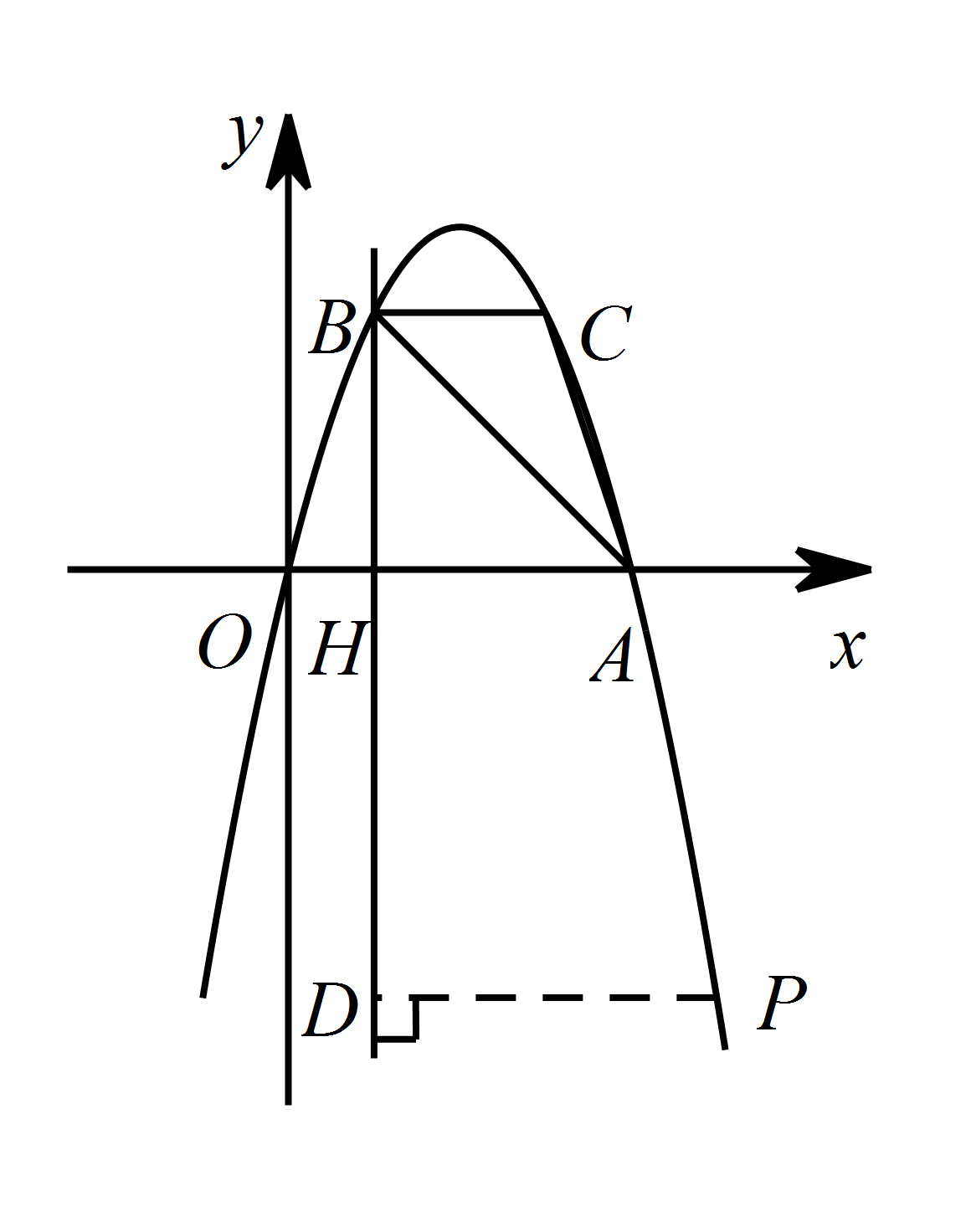设点 $P\left(m,-m^2+4m\right)$．
根据题意得 $BH=AH=3$，$HD=m^2-4m$，$PD=m-1$．
所以 $S_{\triangle ABP}=S_{\triangle ABH}+S_{四边形HAPD}-S_{\triangle BPD}$，
即 $6=\dfrac12\times 3\times 3+\dfrac12\left(3+m-1\right)\left(m^2-4m\right)-\dfrac12\left(m-1\right)\left(3+m^2-4m\right)$，
整理得 $3m^2-15m=0$，
解得 $m_1=0$（舍去），$m_2=5$．
所以点 $P$ 坐标为 $\left(5,-5\right)$． -
若点 $M$ 在直线 $BH$ 上运动，点 $N$ 在 $x$ 轴上运动，当以点 $C,M,N$ 为顶点的三角形为等腰直角三角形时，请直接写出此时 $\triangle CMN$ 的面积．标注答案$ \triangle CMN $ 的面积为 $ \dfrac52 $ 或 $ \dfrac{29}2 $ 或 $ 5 $ 或 $ 17 $解析以点 $C,M,N$ 为顶点的三角形为等腰直角三角形时，分以下多种情况讨论：
① 以点 $M$ 为直角顶点且 $M$ 在 $x$ 轴上方时，$ S_{\triangle CMN}=\dfrac 52 $；
② 以点 $M$ 为直角顶点且 $M$ 在 $x$ 轴下方时，$ S_{\triangle CMN}=\dfrac {29}{2} $；
③ 以点 $N$ 为直角顶点且 $N$ 在 $y$ 轴左侧时，$ S_{\triangle CMN}=17 $；
④ 以点 $N$ 为直角顶点且 $N$ 在 $y$ 轴右侧时，$ S_{\triangle CMN}=5 $；
⑤ 以点 $C$ 为直角顶点时，不能构成满足条件的等腰直角三角形．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
