如图,已知抛物线 $y=ax^2+bx+c$ 与 $x$ 轴交于点 $A,B$,与直线 $AC:y=-x-6$ 交 $y$ 轴于点 $C$,点 $D$ 是抛物线的顶点,且横坐标为 $-2$.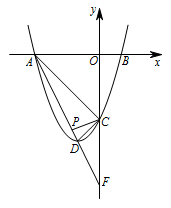

【难度】
【出处】
无
【标注】
-
判断 $\triangle ACD$ 的形状,并说明理由.标注答案$\triangle ACD$ 是直角三角形解析由直线 $AC$ 的解析式为 $y=-x-6$,
可得点 $A$ 的坐标为 $\left(-6,0\right)$,点 $C$ 的坐标为 $\left(0,-6\right)$.
因为抛物线顶点 $D$ 的横坐标是 $-2$,
所以点 $B$ 的坐标为 $\left(2,0\right)$.
把 $A,B,C$ 三点坐标分别代入 $y=ax^2+bx+c$ 中,
有 $\begin{cases}36a-6b+c=0,\\4a+2b+c=0,\\c=-6,\end{cases}$ 解得 $\begin{cases}a=\dfrac12,\\b=2,\\c=-6.\end{cases}$
所以抛物线的解析式是 $y=\dfrac12x^2+2x-6=\dfrac12x^2+2x-6=\dfrac12\left(x+2\right)^2-8$,
所以顶点 $D$ 的坐标是 $\left(-2,-8\right)$.
而 $CD^2=2^2+\left(8-6\right)^2=8$,$AC^2=6^2+6^2=72$,$AD^2=8^2+\left(6-2\right)^2=80$,
所以 $ AD^2=CD^2+AC^2$,
所以 $ \triangle ACD$ 是直角三角形. -
直线 $AD$ 交 $y$ 轴于点 $F$,在线段 $ AD $ 上是否存在一点 $P$,使 $\angle ADC=\angle PCF$.若存在,直接写出点 $P$ 的坐标;若不存在,说明理由.标注答案存在满足条件的点 $P$,其坐标为 $\left(-\dfrac{18}{7},-\dfrac{48}{7}\right)$解析由 $A,D$ 两点的坐标可得直线 $AD$ 的解析式为 $y=-2x-12$.
所以点 $F$ 的坐标为 $\left(0,-12\right)$,得 $CF=6$.
由 $CD$ 两点的坐标可得 $CD=2\sqrt 2$.
设点 $P$ 的坐标为 $\left(x,-2x-12\right)$,则 $ CP^2=x^2+\left(-2x-12+6\right)^2=5x^2+24x+36 $,$ FP^2=x^2+\left(-2x-12+12\right)^2=5x^2 $.
若 $\angle ADC=\angle PCF$,
则 $\angle DCF+\angle DFC=\angle DCF+\angle DCP$,
从而 $\angle PCD=\angle PFC$.
所以 $\triangle PCD\backsim\triangle PFC$,
所以 $\dfrac{PC}{PF}=\dfrac{CD}{CF}$,即 $\dfrac{PC^2}{PF^2}=\dfrac{CD^2}{CF^2}$,
解得 $x=-\dfrac{18}7$ 或 $-\dfrac {18}5 $(舍).
代入解析式可得 $y=-\dfrac{48}7 $.
所以点 $P$ 的坐标为 $\left(-\dfrac{18}7,-\dfrac{48}7\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2