如图,已知抛物线 $y=-x^2+bx+c$ 经过 $A\left(3,0\right),B\left(0,3\right)$ 两点.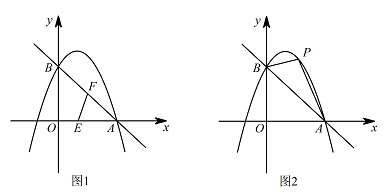

【难度】
【出处】
无
【标注】
-
如图1,动点 $E$ 从 $O$ 点出发,沿着 $OA$ 方向以 $1$ 个单位/秒的速度向终点 $A$ 匀速运动,同时,动点 $F$ 从 $A$ 点出发,沿着 $AB$ 方向以 $\sqrt 2$ 个单位/秒的速度向终点 $B$ 匀速运动,当 $E$,$F$ 中任意一点到达终点时另一点也随之停止运动,连接 $EF$,设运动时间为 $t$ 秒,当 $t$ 为何值时,$\triangle AEF$ 为直角三角形?标注答案$t$ 的值为 $\dfrac {15\left(5-3\sqrt 2\right)}7$ 或 $\dfrac {9\left(5\sqrt 2-3\right)}{41}$解析因为抛物线 $y=-x^2+bx+c$ 经过 $A\left(3,0\right),B\left(0,3\right)$ 两点,
所以 $\begin{cases}-9+3b+c=0,\\c=3.\end{cases}$ 解得 $\begin{cases}b=2,\\c=3.\end{cases}$,
所以抛物线的解析式为 $y=-x^2+2x+3$.
设直线 $AB$ 的解析式为 $y=kx+n$.
所以 $\begin{cases}3k+n=0,\\n=3.\end{cases}$ 解得 $\begin{cases}k=-1,\\n=3.\end{cases}$
所以直线 $AB$ 的解析式为 $y=-x+3$.
由题意得 $OE=t$,$AF=\sqrt 2 t$,
所以 $AE=OA-OE=3-t$.
因为 $\triangle AEF$ 为直角三角形,所以 $\triangle AOB$ 和 $\triangle AEF$ 相似.
① 若 $\triangle AOB\backsim \triangle AEF$,即 $\dfrac {AF}{AB}=\dfrac {AE}{OA}$.
所以 $\dfrac {\sqrt 2t}5=\dfrac {3-t}3 $,解得 $t=\dfrac {15\left(5-3\sqrt 2\right)}7$.
② 若 $\triangle AOB\backsim \triangle AFE$,即 $\dfrac {OA}{AF}=\dfrac {AB}{AE}$.
所以 $\dfrac 3 {\sqrt 2t}=\dfrac 5{3-t}$,解得 $t=\dfrac {9\left(5\sqrt 2-3\right)}{41}$.
综上所述,满足题意的 $t$ 的值为 $\dfrac {15\left(5-3\sqrt 2\right)}7$ 或 $\dfrac {9\left(5\sqrt 2-3\right)}{41}$. -
如图2,取一根橡皮筋,两端点分别固定在 $A$,$B$ 处,用铅笔拉着这根橡皮筋使笔尖 $P$ 在直线 $AB$ 上方的抛物线上移动,动点 $P$ 与 $A$,$B$ 两点构成无数个三角形,在这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时点 $P$ 的坐标;如果不存在,请简要说明理由.标注答案存在面积最大的三角形,最大值是 $\dfrac {27}8$,此时点 $P\left(\dfrac 3 2,\dfrac {15}4\right)$解析过点 $P$ 作 $PC\parallel AB$ 交 $y$ 轴于 $C$,当直线 $PC$ 与 $y=-x^2+2x+3$ 有且只有一个交点时,$\triangle PAB$ 面积最大.
 因为直线 $AB$ 解析式为 $y=-x+3$,故可设直线 $PC$ 解析式为 $y=-x+b$.
因为直线 $AB$ 解析式为 $y=-x+3$,故可设直线 $PC$ 解析式为 $y=-x+b$.
联立方程组 $\begin{cases}y=-x+b,\\y=-x^2+2x+3,\end{cases}$
从而 $x^2-3x+b-3=0$,
所以 $\triangle=9-4\left(b-3\right)=0$,即 $b=\dfrac {21}4$.
解方程组 $\begin{cases}y=-x+\dfrac {21}4,\\y=-x^2+2x+3,\end{cases}$ 得 $\begin{cases}x=\dfrac 3 2,\\y=\dfrac {15}4.\end{cases}$
所以点 $P$ 的坐标为 $\left(\dfrac 3 2,\dfrac {15}4\right)$.
过点 $B$ 作 $BD\perp PC$ 于点 $D$.
显然 $\angle DCB=\angle ABO=45^\circ$,
而 $BC=\dfrac{21}4-3=\dfrac 94$,所以 $BD=\dfrac {9\sqrt 2}8$.
所以 $S_{最大}=\dfrac 1 2AB\cdot BD=\dfrac1 2\times 3\sqrt 2\times \dfrac {9\sqrt 2}8=\dfrac {27}8$.
综上所述,存在面积最大,最大值是 $\dfrac {27}8$,此时点 $P\left(\dfrac 3 2,\dfrac {15}4\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2