如图,在矩形 $OABC$ 中,$OA =5$,$AB =4$,点 $D$ 为边 $AB$ 上一点,将 $\triangle BCD$ 沿直线 $CD$ 折叠,使点 $B$ 恰好落在 $OA$ 边上的点 $E$ 处,分别以 $OC,OA$ 所在的直线为 $x$ 轴、$y$ 轴建立平面直角坐标系.若点 $N$ 在过 $O,D,C$ 三点的抛物线的对称轴上,点 $M$ 在抛物线上,是否存在这样的点 $M$ 与点 $N$,使得以 $M,N,C,E$ 为顶点的四边形是平行四边形?若存在,请求出 $M$ 点的坐标;若不存在,请说明理由.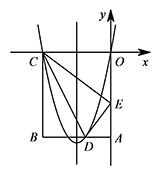
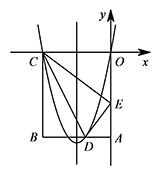
【难度】
【出处】
无
【标注】
【答案】
存在,点 $M$ 的坐标为 $\left(2,16\right)$,$\left(-6,16\right)$ 或 $\left(-2,-\dfrac{16}{3}\right)$
【解析】
由题意可得 $DE=DB=4-AD$,$CE=CB=5$,
从而 $OE=3$,$AE=2$,即点 $E$ 的坐标为 $(0,2)$.
易证 $\triangle DAE\sim \triangle EOC$,
所以 $AD=\dfrac 34AE=\dfrac 32$,即点 $D$ 的坐标为 $\left(\dfrac 32,-5\right)$.
从而过点 $O,D,C$ 的抛物线解析式为 $y=\dfrac 43x^2+\dfrac{16}{3}x$,其对称轴为直线 $ x=-2 $.
由题意可设点 $M$ 的坐标为 $\left(m,\dfrac 43m^2+\dfrac{16}3m\right)$,点 $N$ 的坐标为 $\left(-2,n\right)$.
以 $M,N,C,E$ 为顶点的四边形是平行四边形有如下三种情况:
① 当 $EN,CM$ 为对角线时,有 $\dfrac{x_E+x_N}{2}=\dfrac{x_C+x_M}{2}$,
所以 $\dfrac{0+\left(-2\right)}{2}=\dfrac{m+\left(-4\right)}{2}$,
解得 $m=2$,
所以点 $M$ 的坐标为 $\left(2,16\right)$;
② 当 $EM,CN$ 为对角线时,有 $\dfrac{x_E+x_M}{2}=\dfrac{x_C+x_N}{2}$,
所以 $\dfrac{0+m}{2}=\dfrac{\left(-4\right)+\left(-2\right)}{2}$,
解得 $m=-6$,
所以点 $M$ 的坐标为 $\left(-6,16\right)$;
③ 当 $CE,MN$ 为对角线,有 $\dfrac{x_C+x_E}{2}=\dfrac{x_M+x_N}{2}$,
所以 $\dfrac{(-4)+0}{2}=\dfrac{m+(-2)}{2}$,
解得 $m=-2$
所以点 $M$ 的坐标为 $\left(-2,-\dfrac{16}{3}\right) $.
综上可得,存在满足条件的点 $M$,其坐标为 $\left(2,16\right)$,$\left(-6,16\right)$ 或 $\left(-2,-\dfrac{16}{3}\right)$.
从而 $OE=3$,$AE=2$,即点 $E$ 的坐标为 $(0,2)$.
易证 $\triangle DAE\sim \triangle EOC$,
所以 $AD=\dfrac 34AE=\dfrac 32$,即点 $D$ 的坐标为 $\left(\dfrac 32,-5\right)$.
从而过点 $O,D,C$ 的抛物线解析式为 $y=\dfrac 43x^2+\dfrac{16}{3}x$,其对称轴为直线 $ x=-2 $.
由题意可设点 $M$ 的坐标为 $\left(m,\dfrac 43m^2+\dfrac{16}3m\right)$,点 $N$ 的坐标为 $\left(-2,n\right)$.
以 $M,N,C,E$ 为顶点的四边形是平行四边形有如下三种情况:
① 当 $EN,CM$ 为对角线时,有 $\dfrac{x_E+x_N}{2}=\dfrac{x_C+x_M}{2}$,
所以 $\dfrac{0+\left(-2\right)}{2}=\dfrac{m+\left(-4\right)}{2}$,
解得 $m=2$,
所以点 $M$ 的坐标为 $\left(2,16\right)$;
② 当 $EM,CN$ 为对角线时,有 $\dfrac{x_E+x_M}{2}=\dfrac{x_C+x_N}{2}$,
所以 $\dfrac{0+m}{2}=\dfrac{\left(-4\right)+\left(-2\right)}{2}$,
解得 $m=-6$,
所以点 $M$ 的坐标为 $\left(-6,16\right)$;
③ 当 $CE,MN$ 为对角线,有 $\dfrac{x_C+x_E}{2}=\dfrac{x_M+x_N}{2}$,
所以 $\dfrac{(-4)+0}{2}=\dfrac{m+(-2)}{2}$,
解得 $m=-2$
所以点 $M$ 的坐标为 $\left(-2,-\dfrac{16}{3}\right) $.
综上可得,存在满足条件的点 $M$,其坐标为 $\left(2,16\right)$,$\left(-6,16\right)$ 或 $\left(-2,-\dfrac{16}{3}\right)$.
答案
解析
备注