如图,抛物线与 $x$ 轴交于点 $A(-5,0),B(3,0)$,与 $y$ 轴交于点 $C(0,5)$.有一宽度为 $1$、长度足够的矩形(阴影部分)沿 $x$ 轴方向平移,与 $y$ 轴平行的一组对边交抛物线于点 $P,Q$,交直线 $AC$ 于点 $M,N$.在矩形的平移过程中,当以点 $P,Q,M,N$ 为顶点的四边形是平行四边形时,求点 $M$ 的坐标.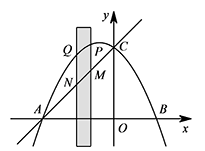

【难度】
【出处】
无
【标注】
【答案】
点 $M$ 的坐标为 $(-2,3)$,$(-2-\sqrt 6,3-\sqrt 6)$ 或 $(-2+\sqrt 6,3+\sqrt 6)$
【解析】
经过点 $A,B,C$ 的抛物线的解析式为 $y=-\dfrac 13x^2-\dfrac 23x+5$,
直线 $AC$ 的解析式为 $y=x+5$.
设点 $M$ 的坐标为 $(t,t+5)$,则点 $N$ 的坐标为 $(t-1,t+4)$,点 $P$ 的坐标为 $\left(t,-\dfrac 13t^2-\dfrac 23t+5\right)$,点 $Q$ 的坐标为 $\left(t-1,-\dfrac 13t^2+\dfrac{16}3\right)$.
在矩形平移的过程中,以 $P,Q,N,M$ 为顶点的平行四边形有两种情况:
① 当点 $P,Q$ 在直线 $AC$ 同侧时,有 $y_P-y_M=y_Q-y_N$,
所以 $-\dfrac 13t^2-\dfrac 23t+5-(t+5)=-\dfrac 13t^2+\dfrac{16}3-(t+4)$,
解得 $t=-2$,
得到点 $M$ 的坐标为 $(-2,3)$;
② 当点 $P,Q$ 在直线 $AC$ 异侧时,有 $y_P-y_M=y_N-y_Q$,
所以 $-\dfrac 13t^2-\dfrac 23t+5-(t+5)=t+4-(-\dfrac 13t^2+\dfrac{16}3)$,
解得 $t=-2\pm \sqrt 6$,
得到点 $M$ 的坐标为 $(-2-\sqrt 6,3-\sqrt 6)$ 或 $(-2+\sqrt 6,3+\sqrt 6)$.
综上可得,满足条件的点 $M$ 的坐标为 $(-2,3)$,$(-2-\sqrt 6,3-\sqrt 6)$ 或 $(-2+\sqrt 6,3+\sqrt 6)$.
直线 $AC$ 的解析式为 $y=x+5$.
设点 $M$ 的坐标为 $(t,t+5)$,则点 $N$ 的坐标为 $(t-1,t+4)$,点 $P$ 的坐标为 $\left(t,-\dfrac 13t^2-\dfrac 23t+5\right)$,点 $Q$ 的坐标为 $\left(t-1,-\dfrac 13t^2+\dfrac{16}3\right)$.
在矩形平移的过程中,以 $P,Q,N,M$ 为顶点的平行四边形有两种情况:
① 当点 $P,Q$ 在直线 $AC$ 同侧时,有 $y_P-y_M=y_Q-y_N$,
所以 $-\dfrac 13t^2-\dfrac 23t+5-(t+5)=-\dfrac 13t^2+\dfrac{16}3-(t+4)$,
解得 $t=-2$,
得到点 $M$ 的坐标为 $(-2,3)$;
② 当点 $P,Q$ 在直线 $AC$ 异侧时,有 $y_P-y_M=y_N-y_Q$,
所以 $-\dfrac 13t^2-\dfrac 23t+5-(t+5)=t+4-(-\dfrac 13t^2+\dfrac{16}3)$,
解得 $t=-2\pm \sqrt 6$,
得到点 $M$ 的坐标为 $(-2-\sqrt 6,3-\sqrt 6)$ 或 $(-2+\sqrt 6,3+\sqrt 6)$.
综上可得,满足条件的点 $M$ 的坐标为 $(-2,3)$,$(-2-\sqrt 6,3-\sqrt 6)$ 或 $(-2+\sqrt 6,3+\sqrt 6)$.
答案
解析
备注