在平面直角坐标系中，已知 $A,B$ 是抛物线 $y=x^2$ 上两个不同的点，其中点 $A$ 在第二象限，点 $B$ 在第一象限，直线 $AB$ 与 $x$ 轴不平行，$\angle AOB=90^\circ$．若直线 $y=-2x-2$ 分别交直线 $AB,y$ 轴于点 $P,C$，直线 $AB$ 交 $y$ 轴于点 $D$，且 $\angle BPC=\angle OCP$，求点 $P$ 的坐标．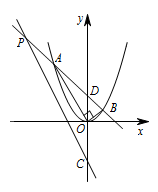
【难度】
【出处】
无
【标注】
【答案】
点 $P$ 的坐标为 $\left(-\dfrac{12}{5},\dfrac{14}{5}\right)$
【解析】
设点 $A$ 的坐标为 $(m,m^2)$，点 $B$ 的坐标为 $(n,n^2)$，其中 $m<0,n>0$．
如图，过点 $A,B$ 分别作 $x$ 轴的垂线，垂足为 $E,F$．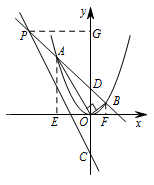
则易证 $\triangle AEO\backsim \triangle OFB$，
所以 $\dfrac{AE}{OF}=\dfrac{OE}{BF}$，即 $\dfrac{m^2}{n}=\dfrac{-m}{n^2}$，
整理得 $mn\left(mn+1\right)=0$．
因为 $mn\neq0$，
所以 $ mn+1=0$，即 $mn=-1$．
设直线 $AB$ 的解析式为 $y=kx+b$．
联立方程组 $\begin{cases}y=kx+b,\\y=x^2,\end{cases}$ 得 $x^2-kx-b=0$．
因为 $ m$，$n$ 是方程得两根，
所以 $ mn=-b$，
所以 $b=1$．
因为直线 $AB$ 与 $y$ 轴交于 $D$，则 $OD=1$．
因为点 $C\left(0,-2\right)$，则 $OC=2$，所以 $ CD=OC+OD=3$．
因为 $\angle BPC=\angle OCP$，
所以 $PD=CD=3$．
设 $P\left(a,-2a-2\right)$，过点 $P$ 作 $PG\perp y$ 轴于点 $G$，则 $PG=-a$，$GD=OG-OD=-2a-3$．
在 $\mathrm {Rt}\triangle PDG$ 中，由勾股定理得 $PG^2+GD^2=PD^2$，
即 $\left(-a\right)^2+\left(-2a-3\right)^2=3^2$，
整理得 $5a^2+12a=0$，
解得 $a_1=0$（舍去），$a_2=-\dfrac{12}{5}$，
当 $a=-\dfrac{12}{5}$ 时，$-2a-2=\dfrac{14}{5}$，
即点 $P$ 的坐标为 $\left(-\dfrac{12}{5},\dfrac{14}{5}\right)$．
如图，过点 $A,B$ 分别作 $x$ 轴的垂线，垂足为 $E,F$．
则易证 $\triangle AEO\backsim \triangle OFB$，所以 $\dfrac{AE}{OF}=\dfrac{OE}{BF}$，即 $\dfrac{m^2}{n}=\dfrac{-m}{n^2}$，
整理得 $mn\left(mn+1\right)=0$．
因为 $mn\neq0$，
所以 $ mn+1=0$，即 $mn=-1$．
设直线 $AB$ 的解析式为 $y=kx+b$．
联立方程组 $\begin{cases}y=kx+b,\\y=x^2,\end{cases}$ 得 $x^2-kx-b=0$．
因为 $ m$，$n$ 是方程得两根，
所以 $ mn=-b$，
所以 $b=1$．
因为直线 $AB$ 与 $y$ 轴交于 $D$，则 $OD=1$．
因为点 $C\left(0,-2\right)$，则 $OC=2$，所以 $ CD=OC+OD=3$．
因为 $\angle BPC=\angle OCP$，
所以 $PD=CD=3$．
设 $P\left(a,-2a-2\right)$，过点 $P$ 作 $PG\perp y$ 轴于点 $G$，则 $PG=-a$，$GD=OG-OD=-2a-3$．
在 $\mathrm {Rt}\triangle PDG$ 中，由勾股定理得 $PG^2+GD^2=PD^2$，
即 $\left(-a\right)^2+\left(-2a-3\right)^2=3^2$，
整理得 $5a^2+12a=0$，
解得 $a_1=0$（舍去），$a_2=-\dfrac{12}{5}$，
当 $a=-\dfrac{12}{5}$ 时，$-2a-2=\dfrac{14}{5}$，
即点 $P$ 的坐标为 $\left(-\dfrac{12}{5},\dfrac{14}{5}\right)$．
答案
解析
备注
