如图,在平面直角坐标系 $xOy$ 中,已知抛物线 $y=x^2+2x-3$ 与 $x$ 轴交于点 $A$,点 $B$(点 $A$ 在点 $B$ 的左边),与 $y$ 轴交于点 $C$,抛物线的顶点为 $M$,过点 $A$ 作 $AN\perp x$ 轴,点 $D$ 为直线 $AC$ 下方抛物线上一点,若 $\angle COD=\angle MAN$,求此时点 $D$ 的坐标.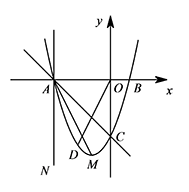
【难度】
【出处】
无
【标注】
【答案】
点 $ D$ 的坐标为 $ \left(-\sqrt{3},-2\sqrt{3} \right)$
【解析】
设点 $D(m,m^2+2m-3)$,所以 $\tan \angle COD=\tan \angle MAN$,即可得到 $m=-\sqrt 3$.
设点 $ D$ 的坐标为 $ \left(m,m^2+2m-3\right)$.
因为 $ \angle COD=\angle MAN$,
所以 $ \tan \angle COD=\tan \angle MAN$.
所以 $ \dfrac {-m} {-\left(m^2+2m-3\right)} =\dfrac 2 4 $.
解得 $ m=\pm \sqrt{3} $.
因为 $ -3<m<0$,
所以 $ m=-\sqrt{3}$.
故点 $ D$ 的坐标为 $ \left(-\sqrt{3},-2\sqrt{3} \right)$.
设点 $ D$ 的坐标为 $ \left(m,m^2+2m-3\right)$.
因为 $ \angle COD=\angle MAN$,
所以 $ \tan \angle COD=\tan \angle MAN$.
所以 $ \dfrac {-m} {-\left(m^2+2m-3\right)} =\dfrac 2 4 $.
解得 $ m=\pm \sqrt{3} $.
因为 $ -3<m<0$,
所以 $ m=-\sqrt{3}$.
故点 $ D$ 的坐标为 $ \left(-\sqrt{3},-2\sqrt{3} \right)$.
答案
解析
备注