抛物线 $ y=ax^2+bx-3a $ 经过 $ A\left(-1,0\right),C\left(0,-3\right) $ 两点，与 $x $ 轴交于另一点 $ B $．点 $ D\left(m,-m-1\right)$ 在第四象限的抛物线上，连接 $BD $，问抛物线上是否存在 $ P $，使 $ \angle PCB=\angle CBD $，若存在求出 $ P $ 点坐标；若不存在，请说明理由．
【难度】
【出处】
无
【标注】
【答案】
存在，点 $P$ 的坐标为 $\left(5,12\right) $，$\left(\dfrac 73,-\dfrac {20}9\right) $
【解析】
如图，当点 $ P $ 在 $ BC $ 上方的抛物线上时，过 $ C$ 作 $ CP\parallel BD $ 交抛物线于点 $ P_1 $，交 $x$ 轴于点 $F$．
将 $A\left(-1,0\right),C\left(0,-3\right)$ 代入 $ y=ax^2+bx-3$，
得 $\begin{cases}a=1,\\b=-2.\end{cases}$
所以抛物线的解析式为 $y=x^2-2x-3$．
将点 $ D\left(m,-m-1\right) $ 代入解析式得 $ m_1=2$，$m_2=-1$（舍负），
所以 $D\left(2,-3\right) $．
因为 $B\left(3,0\right)$，所以直线 $ BD$ 解析式为 $y=3x-9$，
所以直线 $CP_1 $ 解析式为 $y=3x-3$．
与抛物线联立 $ x^2-2x-3 =3x-3$，
解得 $x_1=5 ,x_2=0$（舍），
所以 $P_1\left(5,12\right) $．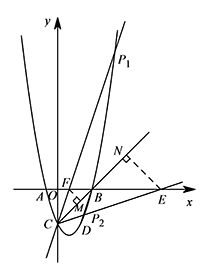
如图，当 $ P_2 $ 在 $ BC $ 下方的抛物线上时，作 $FM\perp CB $ 于 $M $，$ EN\perp CB $ 于 $N $．
因为 $ 3x-3=0$，所以 $ x=1 $，从而 $F\left(1,0\right)$．
所以 $ BF= 2, \angle ABC=45^\circ ,BM=FM=\sqrt 2, BC=3\sqrt 2$
所以 $ CM=2\sqrt 2, CF=\sqrt {10} $．
在 $ {\mathrm{Rt}\triangle BEN} $ 中，$ \angle NBE=45^\circ $，
设 $ BE=\sqrt 2m$，所以 $EN=BN=m$．
因为 $ \angle ECN=\angle DBC=\angle FCB $，
所以 $\dfrac {EN}{CN}= \dfrac {FM}{CM}$，
即 $\dfrac {m}{m+3\sqrt 2}= \dfrac {\sqrt 2}{2\sqrt 2} $，
解得 $m= 3\sqrt 2 $，
所以 $E\left(9,0\right) $，
所以直线 $CE $ 解析式为 $y=\dfrac 13x-3$，
与抛物线联立 $ x^2-2x-3 =\dfrac 13x-3$，
解得 $x_1=\dfrac 73 ,x_2=0$（舍），
所以 $P_2\left(\dfrac 73,-\dfrac {20}9\right) $，
点 $P$ 的坐标为 $\left(5,12\right) $，$\left(\dfrac 73,-\dfrac {20}9\right) $．
将 $A\left(-1,0\right),C\left(0,-3\right)$ 代入 $ y=ax^2+bx-3$，
得 $\begin{cases}a=1,\\b=-2.\end{cases}$
所以抛物线的解析式为 $y=x^2-2x-3$．
将点 $ D\left(m,-m-1\right) $ 代入解析式得 $ m_1=2$，$m_2=-1$（舍负），
所以 $D\left(2,-3\right) $．
因为 $B\left(3,0\right)$，所以直线 $ BD$ 解析式为 $y=3x-9$，
所以直线 $CP_1 $ 解析式为 $y=3x-3$．
与抛物线联立 $ x^2-2x-3 =3x-3$，
解得 $x_1=5 ,x_2=0$（舍），
所以 $P_1\left(5,12\right) $．
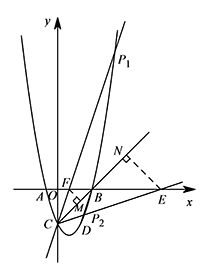如图，当 $ P_2 $ 在 $ BC $ 下方的抛物线上时，作 $FM\perp CB $ 于 $M $，$ EN\perp CB $ 于 $N $．因为 $ 3x-3=0$，所以 $ x=1 $，从而 $F\left(1,0\right)$．
所以 $ BF= 2, \angle ABC=45^\circ ,BM=FM=\sqrt 2, BC=3\sqrt 2$
所以 $ CM=2\sqrt 2, CF=\sqrt {10} $．
在 $ {\mathrm{Rt}\triangle BEN} $ 中，$ \angle NBE=45^\circ $，
设 $ BE=\sqrt 2m$，所以 $EN=BN=m$．
因为 $ \angle ECN=\angle DBC=\angle FCB $，
所以 $\dfrac {EN}{CN}= \dfrac {FM}{CM}$，
即 $\dfrac {m}{m+3\sqrt 2}= \dfrac {\sqrt 2}{2\sqrt 2} $，
解得 $m= 3\sqrt 2 $，
所以 $E\left(9,0\right) $，
所以直线 $CE $ 解析式为 $y=\dfrac 13x-3$，
与抛物线联立 $ x^2-2x-3 =\dfrac 13x-3$，
解得 $x_1=\dfrac 73 ,x_2=0$（舍），
所以 $P_2\left(\dfrac 73,-\dfrac {20}9\right) $，
点 $P$ 的坐标为 $\left(5,12\right) $，$\left(\dfrac 73,-\dfrac {20}9\right) $．
答案
解析
备注
