如图1,二次函数 $y=x^2-2x$ 的图象过点 $A\left(-1,3\right)$,顶点 $B$ 的横坐标为 $1$.点 $P$ 在该二次函数的图象上,点 $Q$ 在 $x$ 轴上,若以 $A,B,P,Q$ 为顶点的四边形是平行四边形,求点 $P$ 的坐标.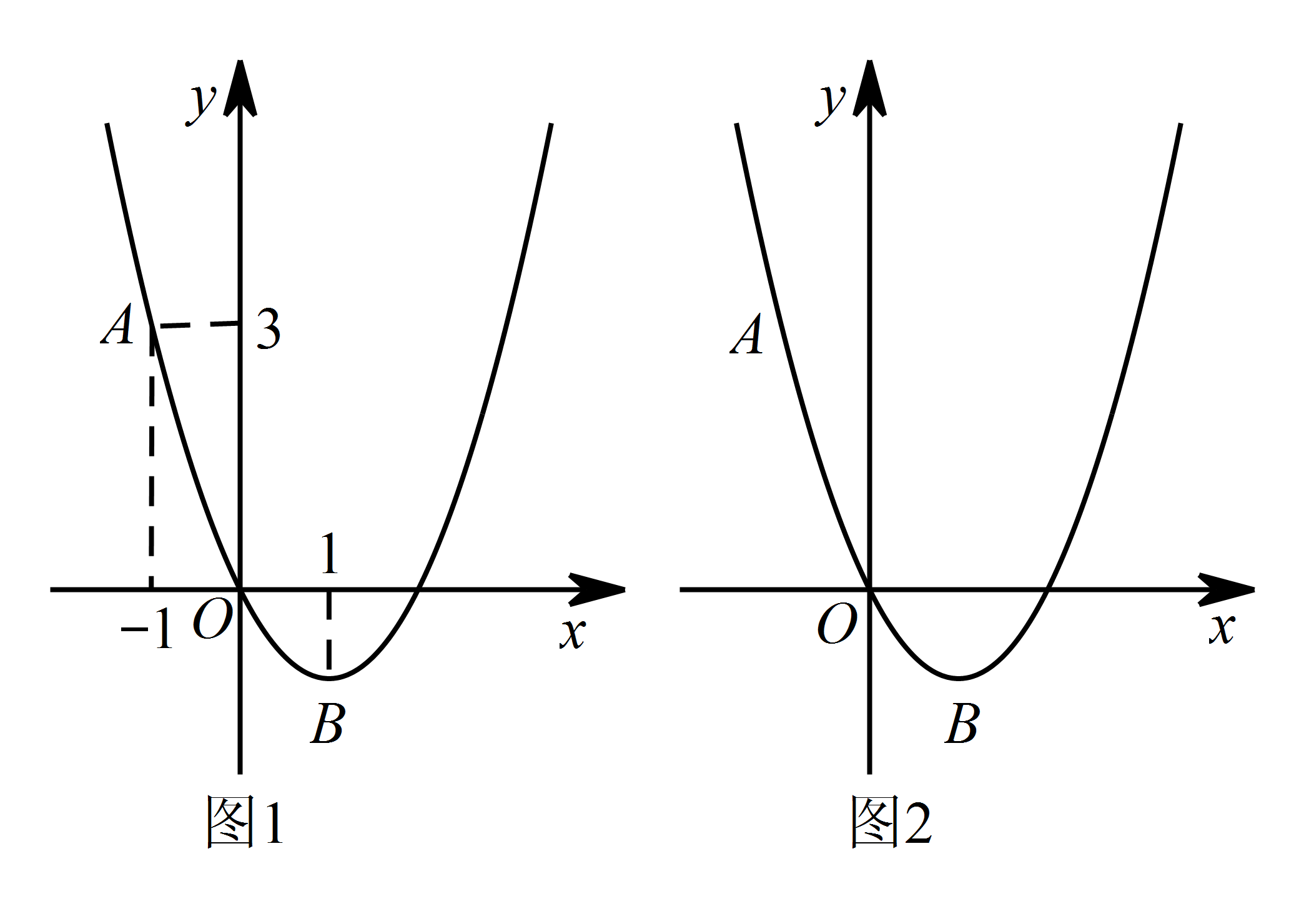

【难度】
【出处】
无
【标注】
【答案】
点 $P$ 的坐标为 $\left(1+\sqrt 3,2\right)$,$\left(1-\sqrt 3,2\right)$,$\left(1+\sqrt 5,4\right)$ 或 $\left(1-\sqrt 5,4\right)$
【解析】
因为点 $A\left(-1,3\right)$,点 $B\left(1,-1\right)$,
所以直线 $AB$ 解析式为 $y=-2x+1$,$AB=2\sqrt 5$,
设点点 $Q\left(m,0\right)$,点 $P\left(n,n^2-2n\right)$.
以 $A,B,P,Q$ 为顶点的四边形是平行四边形有以下可能
① 当 $AB$ 为对角线时,根据中点坐标公式得 $\begin{cases}\dfrac {m+n} 2 =0,\\ \dfrac {n^2-2n} 2 =1,\end{cases}$
解得 $\begin{cases}m=-1-\sqrt 3,\\n=1+\sqrt 3,\end{cases}$ 或 $\begin{cases}m=-1+\sqrt 3,\\n=1-\sqrt 3.\end{cases}$
此时点 $P$ 的坐标为 $\left(1+\sqrt 3,2\right)$ 或 $\left(1-\sqrt 3,2\right)$;
② 当 $AB$ 为边时,根据中点坐标公式得 $\begin{cases}\dfrac {n+1} 2 =\dfrac {m-1} 2 ,\\ \dfrac {n^2-2n-1} 2 =\dfrac 3 2 ,\end{cases}$
解得 $\begin{cases}m=3+\sqrt 5,\\n=1+\sqrt 5,\end{cases}$ 或 $\begin{cases}m=3-\sqrt 5,\\n=1-\sqrt 5.\end{cases}$
此时点 $P$ 的坐标为 $\left(1+\sqrt 5,4\right)$ 或 $\left(1-\sqrt 5,4\right)$.
综上所述,点 $P$ 的坐标为 $\left(1+\sqrt 3,2\right)$,$\left(1-\sqrt 3,2\right)$,$\left(1+\sqrt 5,4\right)$ 或 $\left(1-\sqrt 5,4\right)$.
所以直线 $AB$ 解析式为 $y=-2x+1$,$AB=2\sqrt 5$,
设点点 $Q\left(m,0\right)$,点 $P\left(n,n^2-2n\right)$.
以 $A,B,P,Q$ 为顶点的四边形是平行四边形有以下可能
① 当 $AB$ 为对角线时,根据中点坐标公式得 $\begin{cases}\dfrac {m+n} 2 =0,\\ \dfrac {n^2-2n} 2 =1,\end{cases}$
解得 $\begin{cases}m=-1-\sqrt 3,\\n=1+\sqrt 3,\end{cases}$ 或 $\begin{cases}m=-1+\sqrt 3,\\n=1-\sqrt 3.\end{cases}$
此时点 $P$ 的坐标为 $\left(1+\sqrt 3,2\right)$ 或 $\left(1-\sqrt 3,2\right)$;
② 当 $AB$ 为边时,根据中点坐标公式得 $\begin{cases}\dfrac {n+1} 2 =\dfrac {m-1} 2 ,\\ \dfrac {n^2-2n-1} 2 =\dfrac 3 2 ,\end{cases}$
解得 $\begin{cases}m=3+\sqrt 5,\\n=1+\sqrt 5,\end{cases}$ 或 $\begin{cases}m=3-\sqrt 5,\\n=1-\sqrt 5.\end{cases}$
此时点 $P$ 的坐标为 $\left(1+\sqrt 5,4\right)$ 或 $\left(1-\sqrt 5,4\right)$.
综上所述,点 $P$ 的坐标为 $\left(1+\sqrt 3,2\right)$,$\left(1-\sqrt 3,2\right)$,$\left(1+\sqrt 5,4\right)$ 或 $\left(1-\sqrt 5,4\right)$.
答案
解析
备注