如图，平面直角坐标系 $xOy$ 中，抛物线 $y=x^2-2x-3 $ 与 $ x$ 轴交于点 $ A,B$，与 $y$ 轴交于点 $ C$，抛物线的顶点为 $ D $．直线 $ y=-\dfrac 13x+1 $ 交 $y$ 轴于点 $ E$，求 $ \angle EBC- \angle CBD $ 的度数．
【难度】
【出处】
无
【标注】
【答案】
$ \angle EBC- \angle CBD =45^\circ$
【解析】
过点 $D$ 作 $DH\perp y$ 轴于点 $H$．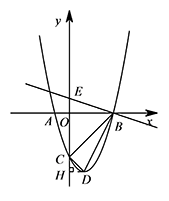
由已知可得 $ A\left(-1,0\right)$，$B\left(3,0\right)$，$C\left(0,-3\right)$，$D\left(1,-4\right)$，$E\left(0,1\right)$．
因为 $ \dfrac {OB}{OC}=\dfrac {CH}{DH} $ 且 $ \angle COB=\angle CHD=90^\circ$，
所以 $\triangle OBC{\backsim }\triangle HCD$，$\angle OCB+\angle HCD=90^\circ$，
所以 $\angle BCD=90^\circ$，$\dfrac {CB}{DC}=\dfrac {OB}{CH}=3 $．
在 $ {\mathrm{Rt}}\triangle BOE $ 中，$ \tan {\angle EBO}=\dfrac 13$，
所以 $\angle EBO=\angle CBD$，
所以 $ \angle EBC- \angle CBD=\angle ABC =45^\circ$．
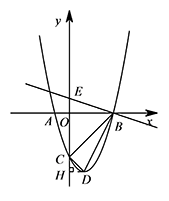由已知可得 $ A\left(-1,0\right)$，$B\left(3,0\right)$，$C\left(0,-3\right)$，$D\left(1,-4\right)$，$E\left(0,1\right)$．因为 $ \dfrac {OB}{OC}=\dfrac {CH}{DH} $ 且 $ \angle COB=\angle CHD=90^\circ$，
所以 $\triangle OBC{\backsim }\triangle HCD$，$\angle OCB+\angle HCD=90^\circ$，
所以 $\angle BCD=90^\circ$，$\dfrac {CB}{DC}=\dfrac {OB}{CH}=3 $．
在 $ {\mathrm{Rt}}\triangle BOE $ 中，$ \tan {\angle EBO}=\dfrac 13$，
所以 $\angle EBO=\angle CBD$，
所以 $ \angle EBC- \angle CBD=\angle ABC =45^\circ$．
答案
解析
备注
