如图，抛物线 $y=ax^2+bx+2$ 经过点 $A(-1,0),B(4,0)$，交 $y$ 轴于点 $C$．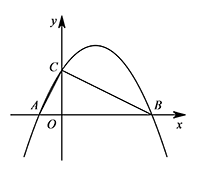
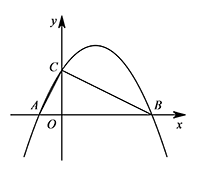
【难度】
【出处】
无
【标注】
-
点 $D$ 在 $y$ 轴右侧抛物线上一点，是否存在点 $D$ 使 $S_{\triangle ABC}=\dfrac 23S_{\triangle ABD}$，若存在请求出点 $D$ 的坐标，若不存在请说明理由；标注答案点 $D$ 的坐标为 $(1,3),(2,3)$ 或 $(5,-3)$解析由题意可得 $\begin{cases}a-b+2=0,\\ 16a+4b+2=0,\end{cases}$ 解得 $\begin{cases}a=-\dfrac 12,\\ b=\dfrac 32.\end{cases}$
所以抛物线的解析式为 $y=-\dfrac 12x^2+\dfrac 32x+2$，点 $C(0,2)$．
令点 $D$ 的坐标为 $\left(m,-\dfrac 12m^2+\dfrac 32m+2\right)$．
由 $S_{\triangle ABC}=\dfrac 23S_{\triangle ABD}$，
可得 $\dfrac 12AB\cdot OC=\dfrac 23\times\dfrac 12AB\cdot \left|-\dfrac 12m^2+\dfrac 32m+2\right|$，
即 $\left|-\dfrac 12m^2+\dfrac 32m+2\right|=3$，
解得 $m_1=1$，$m_2=2$，$m_3=-2$（舍去），$m_4=5$．
所以点 $D$ 的坐标为 $(1,3),(2,3)$ 或 $(5,-3)$． -
将直线 $BC$ 绕点 $B$ 顺时针旋转 $45^\circ$，与抛物线交于另一点 $E$，求 $BE$ 的长．标注答案$BE=\sqrt{10}$解析过点 $C$ 作 $CF\perp BC$，交直线 $BE$ 于点 $F$，过点 $F$ 作 $FH\perp y$ 轴于点 $H$．
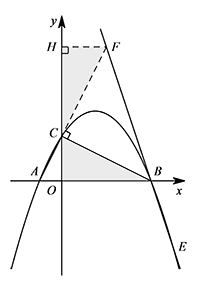由题意可得 $\angle CBF=45^\circ$，则 $CB=CF$．
从而 $\triangle FHC\cong \triangle COB$，
所以 $HF=OC=2$，$HC=OB=4$，
所以点 $F$ 的坐标为 $(2,6)$．
易求直线 $BE$ 的解析式为 $y=-3x+12$．
联立方程组 $\begin{cases}y=-\dfrac 12x^2+\dfrac 32x+2,\\ y=-3x+12.\end{cases}$
解得 $\begin{cases}x_1=4,\\y_1=0,\end{cases}$ $\begin{cases}x_2=5,\\y_2=-3.\end{cases}$
所以点 $E$ 的坐标为 $(5,-3)$，
从而 $BE=\sqrt{(5-4)^2+(-3-0)^2}=\sqrt{10}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
