如图,已知抛物线 $y=-\dfrac 12x^2+2x+6$ 与 $y$ 轴交于点 $A$,与 $x$ 轴交于点 $B$,点 $P$ 是线段 $AB$ 上方抛物线上的一个动点,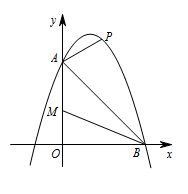
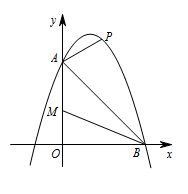
【难度】
【出处】
无
【标注】
-
当点 $P$ 移动到抛物线的什么位置时,使得 $\angle PAB=75^\circ$,求出此时点 $P$ 的坐标;标注答案$P$ 点坐标为 $(4-\dfrac 23\sqrt 3,\dfrac{16}{3}+\dfrac 43\sqrt 3)$解析过点 $P$ 作 $PC\perp y$ 轴,垂足为点 $C$,
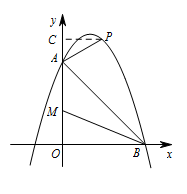 因为 $OA=OB=6$,
因为 $OA=OB=6$,
所以 $\angle OAB=45^\circ$.
当 $\angle PAB=75^\circ$ 时,$\angle PAC=60^\circ$.
因为 $\tan \angle PAC=\dfrac{CP}{AC}$,即所以 $\tan 60^\circ=\dfrac{CP}{AC}=\sqrt 3$.
可设 $AC=m$,那么 $CP=\sqrt 3m$,
所以 $P(\sqrt 3m,6+m)$.
将 $P(\sqrt 3m,6+m)$ 代入 $y=-\dfrac 12x^2+2x+6$,得 $6+m=-\dfrac 12(\sqrt 3m)^2+2\sqrt 3m+6$,
解得 $m_1=0,m_2=\dfrac 43\sqrt 3-\dfrac 23$,
经检验 $P(0,6)$ 与点 $A$ 重合,不合题意,舍去.
所以所求的 $P$ 点坐标为 $(4-\dfrac 23\sqrt 3,\dfrac{16}{3}+\dfrac 43\sqrt 3)$. -
点 $P$ 从 $A$ 点出发沿线段 $AB$ 上方的抛物线向终点 $B$ 移动,在移动中,点 $P$ 的横坐标以每秒 $1$ 个单位长度的速度变动;与此同时点 $M$ 以每秒 $1$ 个单位长度的速度沿 $AO$ 向终点 $O$ 移动,点 $P,M$ 移动到各自终点时停止,当两个动点移动 $t$ 秒时,求四边形 $PAMB$ 的面积 $S$ 关于 $t$ 的函数表达式,并求 $t$ 为何值时,$S$ 有最大值,最大值是多少?标注答案当 $t=-\dfrac {12}{2\times (-\dfrac 32)}=4$ 时,$S_{四边形PAMB}$ 有最大值 $24$解析当两个动点移动 $t$ 秒时,则点 $P(t,-\dfrac 12t^2+2t+6)$,点 $M(0,6-t)$,
作 $PE\perp x$ 轴,垂足为 $E$,$PE$ 交 $AB$ 于点 $F$,则 $EF=EB=6-t$,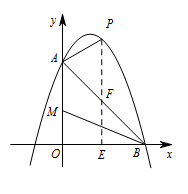 所以 $F(t,6-t)$,
所以 $F(t,6-t)$,
所以 $FP=-\dfrac 12t^2+2t+6-(6-t)=-\dfrac 12t^2+3t$.
因为点 $A$ 到 $PE$ 的距离等于 $OE$,点 $B$ 到 $PE$ 的距离等于 $BE$,
所以 $S_{\triangle PAB}=\dfrac 12FP\cdot OE+\dfrac 12FP\cdot BE=\dfrac 12FP(OE+EB)=\dfrac 12FP\cdot OB=-\dfrac 32t^2+9t$.
又 $S_{\triangle AMB}=S_{\triangle PAB}+S_{\triangle AMB}=-\dfrac 32t^2+12t$,
当 $t=-\dfrac {12}{2\times (-\dfrac 32)}=4$ 时,$S_{四边形PAMB}$ 有最大值 $24$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2