如图，已知抛物线 $y=-\dfrac 13x^2+\dfrac{2}{3}\sqrt 3x+3$ 与坐标轴交于 $A,B,C$ 三点，点 $A$ 在点 $B$ 左侧，点 $C$ 为与 $y$ 轴交点，$\angle BAC$ 的平分线 $AE$ 交 $y$ 轴于点 $D$，交 $BC$ 于点 $E$，过点 $D$ 的直线 $l$ 与射线 $AC,AB$ 分别交于点 $M,N$，证明：当直线 $l$ 绕点 $D$ 旋转时，$\dfrac{1}{AM}+\dfrac{1}{AN}$ 均为定值，并求出该定值．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{\sqrt 3}{2}$
【解析】
设直线 $AC$ 的解析式为 $y=mx+3$，将点 $A$ 的坐标代入得：$-\sqrt 3m+3=0$，解得 $m=\sqrt 3$，
所以直线 $AC$ 的解析式为 $y=\sqrt 3x+3$，
所以 $\angle CAO=60^\circ$，$D(0,1)$．
设直线 $MN$ 的解析式为 $y=kx+1$，
把 $y=0$ 代入 $y=kx+1$ 得：$kx+1=0$，解得 $x=-\dfrac 1k$，
所以点 $N$ 的坐标为 $(-\dfrac 1k,0)$，
所以 $AN=-\dfrac 1k+\sqrt 3=\dfrac{\sqrt 3k-1}{k}$ 。
将 $y=\sqrt 3x+3$ 与 $y=kx+1$ 联立得 $x=\dfrac{2}{k-\sqrt 3}$，
所以点 $M$ 的横坐标为 $\dfrac{2}{k-\sqrt 3}$．
过点 $M$ 作 $MG\perp x$ 轴，垂足为 $G$，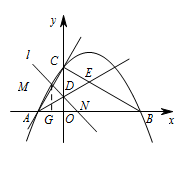
则 $AG=\dfrac{2}{k-\sqrt 3}+\sqrt 3$．
因为 $\angle MAG=60^\circ$，$\angle AGM=90^\circ$，
所以 $AM=2AG=\dfrac{4}{k-\sqrt 3}+2\sqrt 3=\dfrac{2\sqrt 3k-2}{k-\sqrt 3}$，
所以 $\dfrac{1}{AM}+\dfrac{1}{AN}=\dfrac{k-\sqrt 3}{2\sqrt 3k-2}+\dfrac{k}{\sqrt 3k-1}=\dfrac{\sqrt 3}{2}$．
所以直线 $AC$ 的解析式为 $y=\sqrt 3x+3$，
所以 $\angle CAO=60^\circ$，$D(0,1)$．
设直线 $MN$ 的解析式为 $y=kx+1$，
把 $y=0$ 代入 $y=kx+1$ 得：$kx+1=0$，解得 $x=-\dfrac 1k$，
所以点 $N$ 的坐标为 $(-\dfrac 1k,0)$，
所以 $AN=-\dfrac 1k+\sqrt 3=\dfrac{\sqrt 3k-1}{k}$ 。
将 $y=\sqrt 3x+3$ 与 $y=kx+1$ 联立得 $x=\dfrac{2}{k-\sqrt 3}$，
所以点 $M$ 的横坐标为 $\dfrac{2}{k-\sqrt 3}$．
过点 $M$ 作 $MG\perp x$ 轴，垂足为 $G$，
则 $AG=\dfrac{2}{k-\sqrt 3}+\sqrt 3$．因为 $\angle MAG=60^\circ$，$\angle AGM=90^\circ$，
所以 $AM=2AG=\dfrac{4}{k-\sqrt 3}+2\sqrt 3=\dfrac{2\sqrt 3k-2}{k-\sqrt 3}$，
所以 $\dfrac{1}{AM}+\dfrac{1}{AN}=\dfrac{k-\sqrt 3}{2\sqrt 3k-2}+\dfrac{k}{\sqrt 3k-1}=\dfrac{\sqrt 3}{2}$．
答案
解析
备注
