如图，在平面直角坐标系中，直线 $y=\dfrac 12x+2$ 与 $x$ 轴交于点 $A$，与 $y$ 轴交于点 $C$，抛物线 $y=-\dfrac 12x^2-\dfrac 32x+2$ 经过 $A,C$ 两点，与 $x$ 轴的另一交点为点 $B$．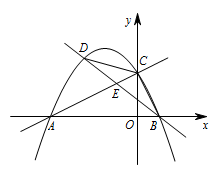
【难度】
【出处】
无
【标注】
-
连接 $BC,CD$，设直线 $BD$ 交线段 $AC$ 于点 $E$，$\triangle CDE$ 的面积为 $S_1$，$\triangle BCE$ 的面积为 $S_2$，求 $\dfrac{S_1}{S_2}$ 的最大值；标注答案$\dfrac{S_1}{S_2}$ 的最大值为 $\dfrac 45$解析如图，令 $y=0$，所以 $-\dfrac 12x^2-\dfrac 32x+2=0$，
所以 $x_1=-4,x_2=1$，所以 $B(1,0)$．
过 $D$ 作 $DM\perp x$ 轴交 $AC$ 于 $M$，过 $B$ 作 $BN\perp x$ 轴交 $AC$ 于 $N$，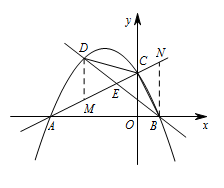
所以 $DM\parallel BN$，
所以 $\triangle DME\cong \triangle BNE$，
所以 $\dfrac{S_1}{S_2}=\dfrac{DE}{BE}=\dfrac{DM}{BN}$．
令 $D(a,-\dfrac 12a^2-\dfrac 32a+2)$，所以 $M(a,\dfrac 12a+2)$．
因为 $B(1,0)$，所以 $N(1,\dfrac 52)$，
所以 $\dfrac{S_1}{S_2}=\dfrac{DM}{BN}=\dfrac{-\dfrac 12a^2-2a}{\dfrac 52}=-\dfrac15(a+2)^2+\dfrac 45$，
所以 $a=-2$ 时 $\dfrac{S_1}{S_2}$ 的最大值为 $\dfrac 45$． -
过点 $D$ 作 $DF\perp AC$，垂足为点 $F$，连接 $CD$，是否存在点 $D$，使得 $\triangle CDF$ 的某个角恰好等于 $\angle BAC$ 的 $2$ 倍？若存在，求点 $D$ 的横坐标；若不存在，请说明理由标注答案存在，$D$ 的横坐标为 $-2$ 或 $-\dfrac{29}{11}$解析因为 $A(-4,0),B(1,0),C(0,2)$，
所以 $AC=2\sqrt 5,BC=\sqrt 5,AB=5$，
所以 $AC^2+BC^2=AB^2$，
所以 $\triangle ABC$ 是以 $\angle ACB$ 为直角的直角三角形，取 $AB$ 的中点 $P$，
所以 $P(-\dfrac 32,0)$，所以 $PA=PC=PB=\dfrac 52$，
所以 $\angle CPO=2\angle BAC$，
所以 $\tan \angle CPO=\tan(2\angle BAC)=\dfrac 43$．
过 $A$ 作 $AQ\perp AC$ 交 $CD$ 延长线于点 $Q$，过 $Q$ 作 $QH\perp x$ 轴于 $H$ \，
所以 $\angle HQA=\angle BAC$，
所以 $\tan \angle HQA=\tan \angle BAC=\dfrac 12$．
令 $AH=m$，所以 $HQ=2m,AQ=\sqrt 5 m$．
情况1：如图 $\angle DCF=2\angle BAC$，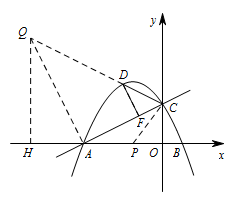
即 $\angle QCA=2\angle BAC$，
所以 $\tan\angle QCA=\dfrac 43$，
所以 $\dfrac{AQ}{AC}=\dfrac{AQ}{2\sqrt 5}=\dfrac 43$，
所以 $AQ=\dfrac{8\sqrt 5}{3}$，
所以 $AH=\dfrac 83$，$HQ=\dfrac{16}{3}$，
所以 $Q(-\dfrac{20}{3},\dfrac{16}{3})$，又因为 $C(0,2)$，
所以直线 $QC$ 解析式为 $y=-\dfrac 12x+2$．
因为 $\begin{cases}y=-\dfrac 12x+2,\\ y=-\dfrac 12x^2-\dfrac 32x+2.\end{cases}$
所以 $\dfrac 12x^2+x=0$，所以 $x_1=0$（舍去），$x_2=-2$，
所以 $x_D=-2$．
情况2：如图 $\angle FDC=2\angle BAC$，即 $\angle AQC=2\angle BAC$，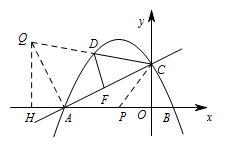
所以 $\tan \angle AQC=\dfrac 43$，
所以 $\dfrac{AC}{AQ}=\dfrac{2\sqrt 5}{AQ}=\dfrac 43$，
所以 $AQ=\dfrac{3\sqrt 5}{2}$，
所以 $AH=\dfrac 32,HQ=3$，
所以 $Q(-\dfrac{11}{2},3)$，又 $C(0,2)$，
所以直线 $QC$ 的解析式为 $y=-\dfrac{2}{11}x+2$．
因为 $\begin{cases}y=-\dfrac {2}{11}x+2,\\ y=-\dfrac 12x^2-\dfrac 32x+2.\end{cases}$
所以 $\dfrac 12x^2+\dfrac{29}{22}x=0$，所以 $x_1=0$（舍去），$x_2=-\dfrac{29}{11}$，
所以 $x_D=-\dfrac{29}{11}$，
综上所述 $D$ 的横坐标为 $-2$ 或 $-\dfrac{29}{11}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
