如图，在平面直角坐标系 $xOy$ 中，抛物线 $C_1:y=-\dfrac{1}{4}x^2+\dfrac{3}{2}x+4$ 与 $y$ 轴交于点 $A$，与 $x$ 轴交于点 $B,C$（点 $B$ 在点 $C$ 的左边）．向右平移抛物线 $C_1$ 使平移的抛物线 $C_2$ 恰好经过 $\triangle ABC$ 的外心，抛物线 $C_2$ 的顶点为 $M$．设点 $P$ 为抛物线 $C_1$ 对称轴上一点，点 $Q$ 为抛物线 $C_1$ 上一点，是否存在以点 $M,Q,P,B$ 为顶点的四边形为平行四边形，若存在，直接写出 $P$ 点坐标，不存在，请说明理由．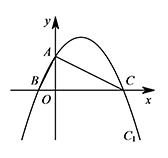
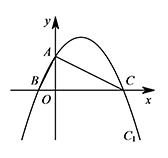
【难度】
【出处】
无
【标注】
【答案】
存在，点 $P$ 的坐标为 $\left(3,0\right)$，$\left(3,-\dfrac{25}{2}\right)$ 或 $\left(3,-25\right)$
【解析】
因为 $y=-\dfrac 14x^2+\dfrac 32x+4=-\dfrac 14(x+2)(x-8)$，
所以点 $A(0,4)$，点 $B(-2,0)$，点 $C(8,0)$．
所以 $\tan\angle ABO=2=\tan\angle CAO$，即 $\angle ABO=\angle CAO$，
从而 $\angle BAC=90^\circ$．
所以 $\triangle ABC$ 的外心即为 $BC$ 的中点，坐标为 $(3,0)$．
故抛物线 $C_1$ 向右平移 $5$ 个单位长度得到抛物线 $C_2$，如图．
易得抛物线 $C_1$ 的顶点坐标为 $\left(3,\dfrac{25}4\right)$，
抛物线 $C_2$ 的顶点 $M$ 的坐标为 $\left(8,\dfrac{25}4\right)$．
由题意可设点 $P$ 的坐标为 $(3,m)$，点 $Q$ 的坐标为 $\left(n,-\dfrac 14n^2+\dfrac 32n+4\right)$．
以点 $M,Q,P,B$ 为顶点的四边形为平行四边形有以下可能：
① 当 $BM$ 为对角线时．
由平行四边形对角线互相平分，可得 $\begin{cases}x_B+x_M=x_P+x_Q,\\y_B+y_M=y_P+y_Q.\end{cases}$
所以 $\begin{cases}-2+8=3+n,\\ 0+\dfrac{25}4=m-\dfrac 14n^2+\dfrac 32n+4,\end{cases}$ 解得 $\begin{cases}m=0,\\n=3.\end{cases}$
即此时点 $P$ 的坐标为 $\left(3,0\right)$；
② 当 $BM$ 为边时．
由平移的性质，可得 $\begin{cases}x_M-x_B=x_P-x_Q,\\y_M-y_B=y_P-y_Q\end{cases} $ 或 $ \begin{cases}x_M-x_B=x_Q-x_P,\\y_M-y_B=y_Q-y_P.\end{cases} $
所以 $ \begin{cases}8+2=3-n,\\\dfrac{25}4-0=m-\left(-\dfrac 14n^2+\dfrac 32n+4\right)\end{cases} $ 或 $ \begin{cases}8+2=n-3,\\\dfrac{25}4-0=\left(-\dfrac 14n^2+\dfrac 32n+4\right)-m,\end{cases} $
解得 $ \begin{cases}m=-\dfrac{25}2,\\ n=-7\end{cases} $ 或 $ \begin{cases}m=-25,\\n=13.\end{cases} $
即此时点 $ P $ 的坐标为 $ \left(3,-\dfrac{25}{2}\right)$ 或 $ P\left(3,-25\right)$．
综上所述，点 $P$ 的坐标为 $\left(3,0\right)$，$\left(3,-\dfrac{25}{2}\right)$ 或 $\left(3,-25\right)$．
所以点 $A(0,4)$，点 $B(-2,0)$，点 $C(8,0)$．
所以 $\tan\angle ABO=2=\tan\angle CAO$，即 $\angle ABO=\angle CAO$，
从而 $\angle BAC=90^\circ$．
所以 $\triangle ABC$ 的外心即为 $BC$ 的中点，坐标为 $(3,0)$．
故抛物线 $C_1$ 向右平移 $5$ 个单位长度得到抛物线 $C_2$，如图．
易得抛物线 $C_1$ 的顶点坐标为 $\left(3,\dfrac{25}4\right)$，抛物线 $C_2$ 的顶点 $M$ 的坐标为 $\left(8,\dfrac{25}4\right)$．
由题意可设点 $P$ 的坐标为 $(3,m)$，点 $Q$ 的坐标为 $\left(n,-\dfrac 14n^2+\dfrac 32n+4\right)$．
以点 $M,Q,P,B$ 为顶点的四边形为平行四边形有以下可能：
① 当 $BM$ 为对角线时．
由平行四边形对角线互相平分，可得 $\begin{cases}x_B+x_M=x_P+x_Q,\\y_B+y_M=y_P+y_Q.\end{cases}$
所以 $\begin{cases}-2+8=3+n,\\ 0+\dfrac{25}4=m-\dfrac 14n^2+\dfrac 32n+4,\end{cases}$ 解得 $\begin{cases}m=0,\\n=3.\end{cases}$
即此时点 $P$ 的坐标为 $\left(3,0\right)$；
② 当 $BM$ 为边时．
由平移的性质，可得 $\begin{cases}x_M-x_B=x_P-x_Q,\\y_M-y_B=y_P-y_Q\end{cases} $ 或 $ \begin{cases}x_M-x_B=x_Q-x_P,\\y_M-y_B=y_Q-y_P.\end{cases} $
所以 $ \begin{cases}8+2=3-n,\\\dfrac{25}4-0=m-\left(-\dfrac 14n^2+\dfrac 32n+4\right)\end{cases} $ 或 $ \begin{cases}8+2=n-3,\\\dfrac{25}4-0=\left(-\dfrac 14n^2+\dfrac 32n+4\right)-m,\end{cases} $
解得 $ \begin{cases}m=-\dfrac{25}2,\\ n=-7\end{cases} $ 或 $ \begin{cases}m=-25,\\n=13.\end{cases} $
即此时点 $ P $ 的坐标为 $ \left(3,-\dfrac{25}{2}\right)$ 或 $ P\left(3,-25\right)$．
综上所述，点 $P$ 的坐标为 $\left(3,0\right)$，$\left(3,-\dfrac{25}{2}\right)$ 或 $\left(3,-25\right)$．
答案
解析
备注
