如图，在平面直角坐标系中，抛物线 $y=ax^2+bx+c$ 的顶点坐标为 $\left(2,9\right)$，与 $y$ 轴交于点 $A\left(0,5\right)$，与 $x$ 轴交于点 $E,B$．
【难度】
【出处】
无
【标注】
-
过点 $A$ 作 $AC$ 平行于 $x$ 轴，交抛物线于点 $C$，点 $P$ 为抛物线上的一点（点 $P$ 在 $AC$ 上方），作 $PD$ 平行与 $y$ 轴交 $AB$ 于点 $D$，问当点 $P$ 在何位置时，四边形 $APCD$ 的面积最大？并求出最大面积；标注答案四边形 $APCD$ 面积最大值为 $\dfrac {25} 2$解析当 $y=0$ 时，$-x^2+4x+5=0$，
所以 $x_1=-1$，$x_2=5$，
所以点 $E\left(-1,0\right)$，点 $B\left(5,0\right)$．
从而直线 $AB$ 的解析式为 $y=-x+5$．
设点 $P\left(x,-x^2+4x+5\right)$，则点 $ D\left(x,-x+5\right)$，
所以 $PD=-x^2+4x+5+x-5=-x^2+5x$．
所以 $ S_{四边形APCD}=\dfrac 12 \cdot AC\cdot PD=2\left(-x^2+5x\right)=-2x^2+10x$，
所以当 $x=-\dfrac {10} {2\times \left(-2\right)} =\dfrac 5 2$ 时，四边形 $APCD$ 面积最大，最大值为 $S=\dfrac {25} 2$． -
若点 $M$ 在抛物线上，点 $N$ 在其对称轴上，使得以 $A,E,N,M$ 为顶点的四边形是平行四边形，且 $AE$ 为其一边，求点 $M,N$ 的坐标．标注答案当 $M$ 点的坐标为 $\left(1,8\right)$ 时，$N$ 点坐标为 $\left(2,13\right)$；
当 $M$ 点的坐标为 $\left(3,8\right)$ 时，$N$ 点坐标为 $\left(2,3\right)$解析如图，过点 $M$ 作 $MH$ 垂直于对称轴，垂足为点 $H$．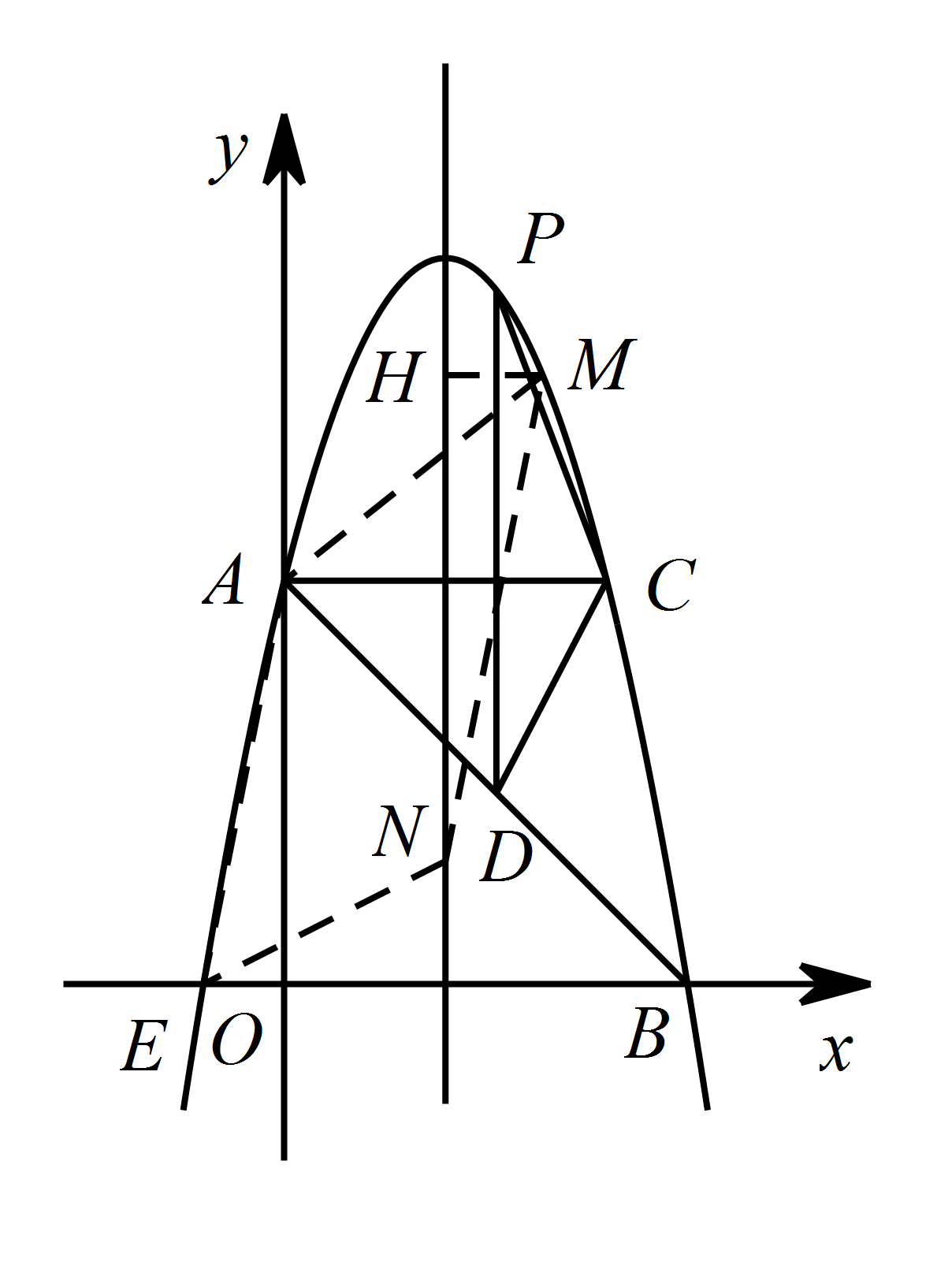
因为 $MN\parallel AE$，$MN=AE$，
所以 $\triangle HMN\cong \triangle AOE$，
所以 $HM=OE=1$，
所以 $M$ 点的横坐标为 $x=3$ 或 $x=1$．
当 $x=1$ 时，$M$ 点纵坐标为 $8$，
当 $x=3$ 时，$M$ 点纵坐标为 $8$，
所以 $M$ 点的坐标为 $\left(1,8\right)$ 或 $\left(3,8\right)$．
因为点 $A\left(0,5\right)$，点 $E\left(-1,0\right)$，
所以直线 $AE$ 解析式为 $y=5x+5$．
因为 $MN\parallel AE$，
所以 $MN$ 的解析式为 $y=5x+b$．
因为点 $N$ 在抛物线对称轴 $x=2$ 上，
所以 $N\left(2,10+b\right)$．
因为 $AE^2=OA^2+OE^2=26$，$MN=AE$，
所以 $1+\left(b+2\right)^2=26$，
解得 $b=3$ 或 $b=-7$，
所以 $N$ 点的坐标为 $\left(2,3\right)$ 或 $\left(2,13\right)$．
综上可得，当 $M$ 点的坐标为 $\left(1,8\right)$ 时，$N$ 点坐标为 $\left(2,13\right)$，
当 $M$ 点的坐标为 $\left(3,8\right)$ 时，$N$ 点坐标为 $\left(2,3\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
