如图，抛物线 $ y=x^{2}-4x-5 $ 经过点 $ A\left(4, -5\right) $，与 $ x $ 轴的负半轴交于点 $ B $，与 $ y $ 轴交于点 $ C $，且 $OC=5OB$，抛物线的顶点为点 $ D $．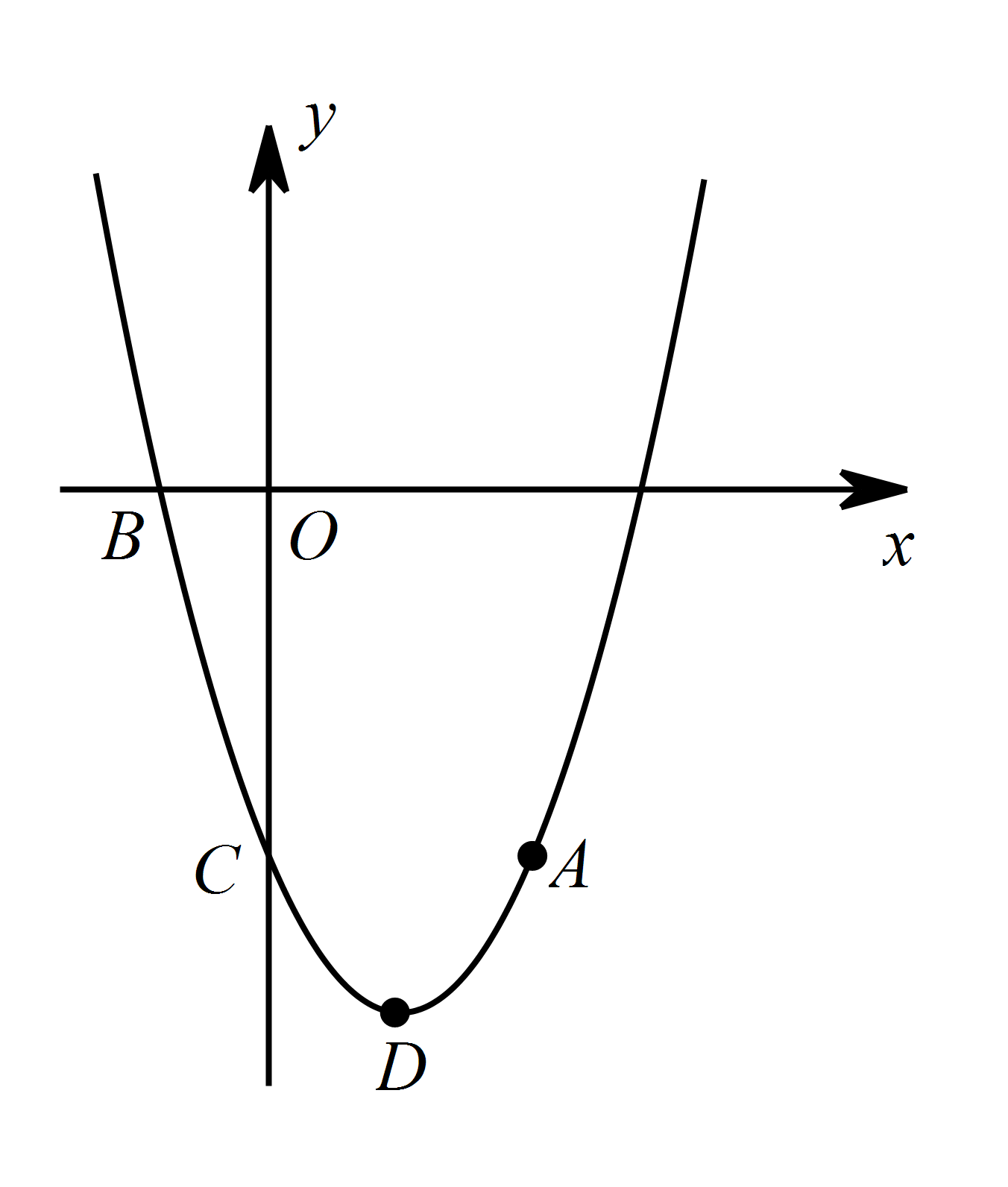
【难度】
【出处】
无
【标注】
-
联结 $ AB $，$ BC $，$ CD $，$ DA $，求四边形 $ ABCD $ 的面积；标注答案$ S_{四边形ABCD}=18 $解析由 $ y=x^{2}-4x-5 $，得顶点 $ D $ 的坐标是 $ \left(2,-9\right) $．
联结 $ AC $．
因为点 $ A $ 的坐标是 $ \left(4,-5\right) $，点 $ C $ 的坐标是 $ \left(0,-5\right) $，
又 $ S_{\triangle ABC}=\dfrac{1}{2 }\times 4\times 5=10 $，$ S_{\triangle ACD}=\dfrac{1}{2 }\times 4\times 4=8 $，
所以 $ S_{四边形ABCD}=S_{\triangle ABC}+S_{\triangle ACD}=18 $． -
如果点 $ E $ 在 $ y $ 轴的正半轴上，且 $ \angle BEO=\angle ABC $，求点 $ E $ 的坐标．标注答案点 $ E $ 的坐标为 $ \left(0,\dfrac{3}{ 2}\right) $解析过点 $ C $ 作 $ CH\perp AB $，垂足为点 $ H $．
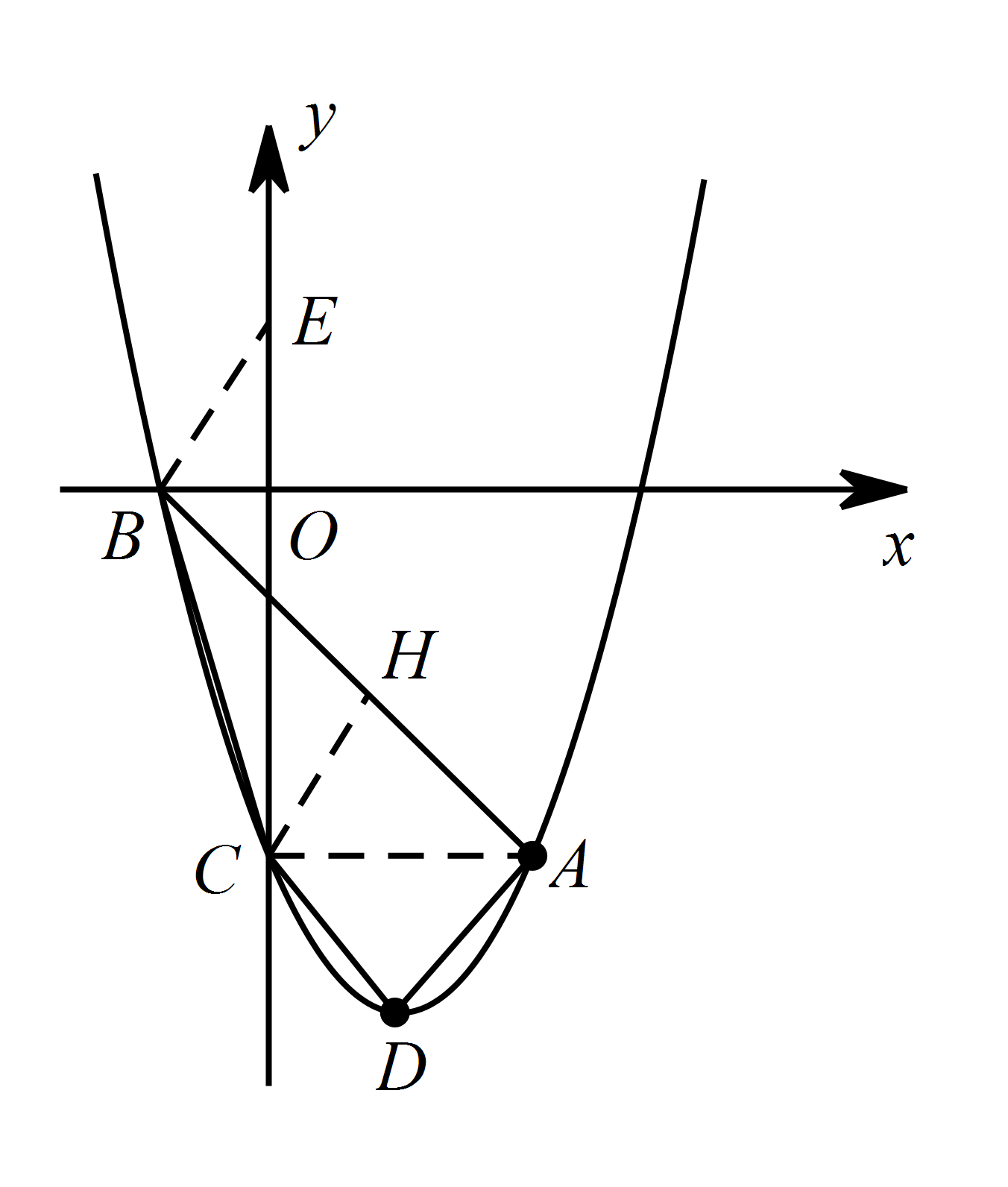因为 $ S_{\triangle ABC}=\dfrac{1}{2 }\times AB\times CH=10 $，$ AB=5\sqrt{2} $，
所以 $ CH=2\sqrt{2} $．
在 $ \mathrm {Rt}\triangle BCH $ 中，$ \angle BHC=90^{\circ} $，$ BC=\sqrt{26} $，$ BH=\sqrt{BC^{2}-CH^{2}}=3\sqrt{2} $，
所以 $ \tan \angle CBH=\dfrac{CH}{BH }=\dfrac{2}{3 } $．
在 $ \mathrm {Rt}\triangle BOE $ 中，$ \angle BOE=90^{\circ} $，$ \tan \angle BEO=\dfrac{BO}{EO } $．
因为 $ \angle BEO=\angle ABC $，
所以 $ \dfrac{BO}{EO }=\dfrac{2}{ 3} $，得 $ EO=\dfrac{3}{2 } $，
所以点 $ E $ 的坐标为 $ \left(0,\dfrac{3}{ 2}\right) $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
