如图，平面直角坐标系 $xOy$ 中，菱形 $ABCD$ 的中心与原点重合，$C,D$ 两点的坐标分别为 $\left(4,0\right),\left(0,3\right)$．现有两动点 $P,Q$ 分别从 $A,C$ 同时出发，点 $P$ 沿线段 $AD$ 向终点 $D$ 运动，点 $Q$ 沿折线 $CBA$ 向终点 $A$ 运动，设运动时间为 $t$ 秒．
【难度】
【出处】
无
【标注】
-
菱形 $ABCD$ 的边长是 $\underline{\qquad}$，面积是 $\underline{\qquad}$，高 $BE$ 的长是 $\underline{\qquad}$；标注答案$5$；$24$；$\dfrac {24}5$解析略
-
若点 $P$ 的速度为每秒 $1$ 个单位，点 $Q$ 的速度为每秒 $k$ 个单位，在运动过程中，任何时刻都有相应的 $k$ 值，使得 $\triangle APQ$ 沿它的一边翻折，翻折前后两个三角形组成的四边形为菱形，请探究当 $t=4$ 秒时的情形，并求出 $k$ 的值．标注答案满足条件的 $k$ 值为 $\dfrac 32,\dfrac {11}{10},\dfrac {97}{50}$解析要使 $\triangle APQ$ 沿它的一边翻折，翻折前后的两个三角形组成的四边形为菱形，根据轴对称的性质，翻折前后两个图形是全等的，所以要满足四边形是菱形只需 $\triangle APQ$ 为等腰三角形即可．当 $t=4$ 时，$AP=4$．
① 如图，当点 $Q$ 在线段 $BC$ 上时，$PQ\geqslant BE>AP$，同理 $AQ>AP$，所以只存在 $QA=QP$ 时的等腰三角形．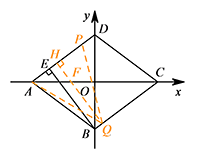
过点 $Q$ 作 $QH\perp AP$ 于点 $H$，交 $AC$ 于点 $F$，则 $ AH=PH=\dfrac 12AP=2 $．
易证 $\triangle AFH\backsim \triangle CFQ\backsim \triangle ADO $，
所以 $\dfrac {FH}{AH}=\dfrac {FQ}{CQ}=\dfrac {DO}{AO}=\dfrac {3}{4}$，
可得 $FH=\dfrac {3}{2}$，$FQ=\dfrac {33}{10}$，$CQ=\dfrac {22}{5}$．
从而 $k=\dfrac{CQ}4=\dfrac {11}{10}$；
② 当点 $Q$ 在 $BA$ 上时，有两种情况的等腰三角形存在：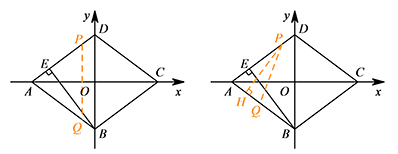
（i）如图1，当 $AP=AQ$ 时，此时点 $P,Q$ 关于 $x$ 轴对称，$BQ=PD=1$．
所以 $k=\dfrac{CB+BQ}4=\dfrac 32$；
（ii）如图2，当 $PA=PQ$ 时，过点 $P$ 作 $PH\perp AB$ 于点 $H$．
易证 $\triangle AHP\backsim \triangle AEB$，
所以 $\dfrac {AH}{AE}=\dfrac {AP}{AB}$，
其中 $AE=\sqrt {{AB^2}-{BE}^2}= \dfrac 75$，
所以 $AH=\dfrac {28}{25}$，$AQ=2AH=\dfrac {56}{25}$．
所以 $k=\dfrac{CB+BQ}4=\dfrac {97}{50}$；
（iii）由 ① 可得，$AP$ 的垂直平分线与 $BC$ 相交，所以点 $Q$ 在线段 $AB$ 上时，不存在 $AQ=PQ$ 这种情况．
综上所得，满足条件的 $k$ 值为 $\dfrac 32,\dfrac {11}{10},\dfrac {97}{50}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
