如图,二次函数 $y=\dfrac 12x^2-x+c$ 的图象与 $x$ 轴分别交于 $A,B$ 两点,顶点 $M$ 关于 $x$ 轴的对称点是 $M'$.问是否存在抛物线 $y=\dfrac 12x^2-x+c$,使得四边形 $AMBM'$ 为正方形?若存在,请求出此抛物线的函数关系式;若不存在,请说明理由.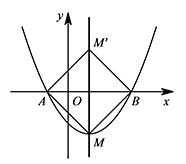
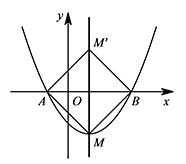
【难度】
【出处】
无
【标注】
【答案】
存在抛物线 $y=\dfrac 12x^2-x-{\dfrac 32}$,使得四边形 $AMBM'$ 为正方形
【解析】
易得 $AMBM'$ 是菱形,所以当 $AB=MM'$ 时,四边形 $AMBM'$ 是正方形.
设点 $A$ 的坐标为 $\left(x_1,0\right)$,点 $B$ 的坐标为 $\left(x_2,0\right)$.
令 $\dfrac 12x^2-x+c =0$,
所以 $x_1+x_2=2$,$x_1\cdot x_2=2c$,
所以 $AB=\sqrt {\left(x_1+{x_2}\right)^2-4{x_1}{x_2}}=\sqrt {4-8c}$,
点 $M$ 的纵坐标为 $\dfrac {4ac-b^2}{4a}=\dfrac {2c-1}2$.
若四边形 $AMBM'$ 为正方形,则有 $\sqrt {4-8c}=2\times \left|{\dfrac {2c-1}2}\right|$,
解得 $c_1=\dfrac 12$,$c_2=-\dfrac 32$,
又抛物线与 $x$ 轴有两个交点,
所以 $\Delta =b^2-4ac=\left(-1\right)^2-4\times {\dfrac 12}c>0$,
解得 $c<\dfrac 12$.
所以 $c$ 的值为 $-\dfrac 32$.
所以存在抛物线 $y=\dfrac 12x^2-x-{\dfrac 32}$,使得四边形 $AMBM'$ 为正方形.
设点 $A$ 的坐标为 $\left(x_1,0\right)$,点 $B$ 的坐标为 $\left(x_2,0\right)$.
令 $\dfrac 12x^2-x+c =0$,
所以 $x_1+x_2=2$,$x_1\cdot x_2=2c$,
所以 $AB=\sqrt {\left(x_1+{x_2}\right)^2-4{x_1}{x_2}}=\sqrt {4-8c}$,
点 $M$ 的纵坐标为 $\dfrac {4ac-b^2}{4a}=\dfrac {2c-1}2$.
若四边形 $AMBM'$ 为正方形,则有 $\sqrt {4-8c}=2\times \left|{\dfrac {2c-1}2}\right|$,
解得 $c_1=\dfrac 12$,$c_2=-\dfrac 32$,
又抛物线与 $x$ 轴有两个交点,
所以 $\Delta =b^2-4ac=\left(-1\right)^2-4\times {\dfrac 12}c>0$,
解得 $c<\dfrac 12$.
所以 $c$ 的值为 $-\dfrac 32$.
所以存在抛物线 $y=\dfrac 12x^2-x-{\dfrac 32}$,使得四边形 $AMBM'$ 为正方形.
答案
解析
备注