如图，已知抛物线经过原点 $O$ 和 $x$ 轴上一点 $A\left(4,0\right)$，抛物线顶点为 $E$，它的对称轴与 $x$ 轴交于点 $D$．直线 $y=-2x-1$ 经过抛物线上一点 $B\left(-2,m\right)$，与抛物线的对称轴交于点 $F$．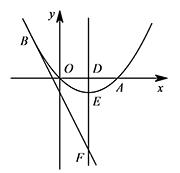
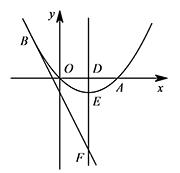
【难度】
【出处】
无
【标注】
-
求抛物线的解析式；标注答案抛物线的解析式为 $y=\dfrac 14x^2-x$解析因为点 $B\left(-2,m\right)$ 在直线 $y=-2x-1$ 上，
所以 $m=3$，从而 $B\left(-2,3\right)$．
由抛物线经过原点 $O$，可设抛物线的解析式为 $y=ax^2+bx $．
将 $A\left(4,0\right),B\left(-2,3\right)$ 的坐标代入解析式，得 $\begin{cases} 4a-2b=3,\\ 16a+4b=0.\end{cases}$
解得 $\begin{cases} a=\dfrac 14,\\ b=-1.\end{cases}$
所以该抛物线的解析式为 $y=\dfrac 14x^2-x$． -
点 $Q$ 是平面内任意一点，点 $M$ 从点 $F$ 出发，沿对称轴向上以每秒 $1$ 个单位长度的速度匀速运动，设点 $M$ 的运动时间为 $t$ 秒，是否能使以 $Q,A,E,M$ 四点为顶点的四边形是菱形．若能，请直接写出点 $M$ 的运动时间 $t$ 的值；若不能，请说明理由．标注答案能，$t$ 的值为 $4-\sqrt 5,6,4+\sqrt 5$ 或 $\dfrac {13}2$解析易得抛物线的顶点 $E$ 的坐标为 $\left(2,-1\right)$，对称轴为 $x=2$，
所以点 $F$ 坐标为 $\left(2,-5\right)$，
从而 $DF=5$，$AE=\sqrt 5$．
如图，在点 $M$ 的运动过程中，以 $Q,A,E,M$ 为顶点的四边形是菱形有以下四种情况：
① 对于菱形 $AEM_1Q_1$，此时 $EM_1 =AE=\sqrt 5$，
所以 $FM_1=DF-DE-EM_1=4-\sqrt 5$，
所以 $t_1=4-\sqrt 5$；
② 对于菱形 $AEQ_2M_2$，此时 $DM_2=DE=1$，
所以 $FM_2=DF+DM_2=6$，
所以 $t_2=6$；
③ 对于菱形 $AEM_3Q_3$，此时 $EM_3=AE=\sqrt 5$，
所以 $DM_3=EM_3-DE=\sqrt 5-1$，
所以 $FM_3=DM_3+FD=4+\sqrt 5$，
所以 $t_3=4+\sqrt 5$；
④ 对于菱形 $ AM_4EQ_4 $，此时 $AE$ 为菱形的对角线．
设对角线 $AE$ 与 $M_4Q_4$ 交于点 $H$，则 $AE\perp M_4Q_4$．
由 $\triangle AED\backsim \triangle M_4EH$，可得 $\dfrac {M_4E}{AE}=\dfrac {EH}{DE}$，
所以 ${M_4E}=\dfrac 52$，
所以 $DM_4=M_4E-DE=\dfrac 32$，$M_4F=DM_4+DF=\dfrac {13}2$，
所以 $t_4=\dfrac {13}2$．
综上可得，存在点 $M,Q$，使得以 $Q,A,E,M$ 四点为顶点的四边形是菱形，$t$ 的值为 $4-\sqrt 5,6,4+\sqrt 5$ 或 $\dfrac {13}2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
