如图，已知直线 $l:y=\dfrac43x+4$ 与 $x$ 轴，$y$ 轴分别交于点 $A,B$，$\odot O$ 的半径为 $1$，点 $C$ 是 $y$ 轴正半轴上的一个点，如果 $\odot C$ 与 $\odot O$ 相切，又与直线 $l$ 相切，求圆心 $C$ 的坐标．
【难度】
【出处】
无
【标注】
【答案】
点 $C$ 的坐标为 $(0,\dfrac{17}{8})$ 或 $C(0,\dfrac{7}{8})$
【解析】
如图所示，过点 $C$ 作 $CD\perp AB$，垂足为 $D$．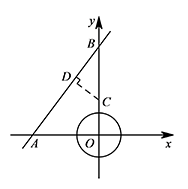
易证 $\triangle CDB\sim \triangle AOB$，
所以 $\dfrac{CD}{CB}=\dfrac{AO}{AB}=\dfrac 35$．
设 $CD=3m$，$BC=5m$，
则点 $C$ 坐标为 $(0,4-5m)$，$\odot C$ 的半径为 $3m$，
所以 $\odot O$ 与 $\odot C$ 的圆心距为 $d=OC=4-5m$．
① 如图，当两圆外切时，有 $3m+1=4-5m$，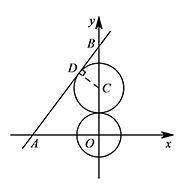
解得 $m=\dfrac 38.$ 此时 $C\left(0,\dfrac{17}{8}\right)$；
② 如图，当两圆内切时，有 $3m-1=4-5m,$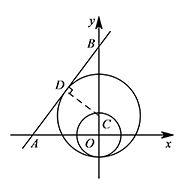
解得 $m=\dfrac 58$．此时 $C\left(0,\dfrac{7}{8}\right)$．
综上可得，满足题意的圆心 $C$ 的坐标为 $(0,\dfrac{17}{8})$ 或 $C(0,\dfrac{7}{8})$．
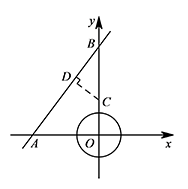易证 $\triangle CDB\sim \triangle AOB$，所以 $\dfrac{CD}{CB}=\dfrac{AO}{AB}=\dfrac 35$．
设 $CD=3m$，$BC=5m$，
则点 $C$ 坐标为 $(0,4-5m)$，$\odot C$ 的半径为 $3m$，
所以 $\odot O$ 与 $\odot C$ 的圆心距为 $d=OC=4-5m$．
① 如图，当两圆外切时，有 $3m+1=4-5m$，
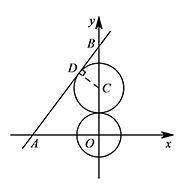解得 $m=\dfrac 38.$ 此时 $C\left(0,\dfrac{17}{8}\right)$；② 如图，当两圆内切时，有 $3m-1=4-5m,$
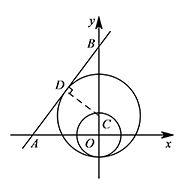解得 $m=\dfrac 58$．此时 $C\left(0,\dfrac{7}{8}\right)$．综上可得，满足题意的圆心 $C$ 的坐标为 $(0,\dfrac{17}{8})$ 或 $C(0,\dfrac{7}{8})$．
答案
解析
备注
